题目内容
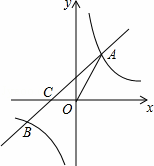
如图,一次函数y=x+b的图象与反比例函数y= 的图象交于点A和点B(﹣2,n),与x轴交于点C(﹣1,0),连接OA.
的图象交于点A和点B(﹣2,n),与x轴交于点C(﹣1,0),连接OA.
(1)求一次函数和反比例函数的解析式;
(2)若点P在坐标轴上,且满足PA=OA,求点P的坐标.
解:(1)∵一次函数y=x+b的图象与x轴交于点C(﹣1,0),
∴﹣1+b=0 ,解得b=1,
,解得b=1,
∴一次函数的解析式为y=x+1,
∵一次函数y=x+1的图象过点B(﹣2,n),
∴n=﹣2+1=﹣1,
∴B(﹣2,﹣1).
∵反比例函数y= 的图象过点B(﹣2,﹣1),
的图象过点B(﹣2,﹣1),
∴k=﹣2×(﹣1)=2,
∴反比例函数的解析式为y= ;
;
(2)由 ,解得
,解得 ,或
,或 ,
,
∵B(﹣2,﹣1),
∴A(1,2).
分两种情况:
①如果点P在x轴上,设点P的坐标为(x,0),
∵PA=OA,
∴(x﹣1)2+22=12+22,
解得x1=2,x2=0(不合题意舍去),
∴点P的坐标为(2,0);
②如果点P在y轴上,设点P的坐标为(0,y),
∵PA=OA,
∴12+(y﹣2)2=12+22,
解得y1=4,y2=0(不合题意舍去),
∴点P的坐标为(0,4);
综上所述,所求点P的坐标为(2,0)或(0,4).

练习册系列答案
相关题目
 ÷(a﹣
÷(a﹣ ),其中a,b满足|a﹣3|+(b﹣2)2=0.
),其中a,b满足|a﹣3|+(b﹣2)2=0.

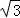 ,PA=
,PA=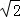 ,则:
,则: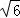 ,PC= 2 ;
,PC= 2 ;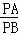 =
=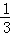 ,求
,求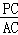 的值.(提示:请利用备用图进行探求)
的值.(提示:请利用备用图进行探求) 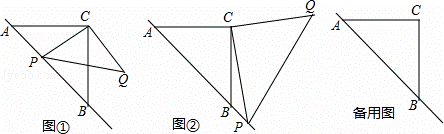

 B.中位数是6 C.众数是4 D.方差是3.2
B.中位数是6 C.众数是4 D.方差是3.2 别在x轴,y轴正半轴上,直线
别在x轴,y轴正半轴上,直线 交边BC于点M(m,n)(m<n),
交边BC于点M(m,n)(m<n),
 (
( )交边AB于点N.若△OAN
)交边AB于点N.若△OAN 的面积是4,求△OMN的面积.
的面积是4,求△OMN的面积.