题目内容
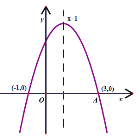
【题目】在平面直角坐标系xOy中，直线y＝﹣x+1与图数y＝
的限象交于A（﹣2，a），B两点．
（1）写出a，k的值________；
（2）已知点P（0，n），过点P作平行于x轴的直线l，交函数y＝的图象于点 C（x1， y1），交直线 y＝﹣x+1的图象于点 D（x2，y2），若|x1|≤|x2|，结合函数图象，请写出 m的取值范围________．
【答案】】a=3，
；； 
或
．
【解析】
（1）将点
代入
，得出点
的坐标，再代入函数
，即可求出
的值；
（2）求出点
的坐标，结合函数的图象即可求解．
解：（1）
直线与函数的图象交于，
把代入
解得
，
．
把
代入，
解得；
（2）画出函数图象如图
解
得
或
，
，
，
根据图象可得：若
，则或．
故答案为：（1）a=3，；（2）或．
练习册系列答案
阅读快车系列答案
相关题目
