Question

【题目】已知该抛物线y=x2+bx+c，经过点B（-4，0）和点A（1，0）与y轴交于点C．

（1）确定抛物线的表达式，并求出C点坐标；

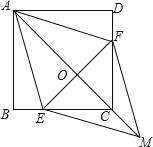
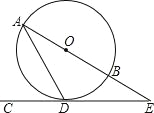
（2）如图1，经过点B的直线l交抛物线于点E，且满足∠EBO=∠ACB，求出所有满足条件的点E的坐标，并说明理由；

（3）如图2，M，N是抛物线上的两动点（点M在左，点N在右），分别过点M，N作PM∥x轴，PN∥y轴，PM，PN交于点P．点M，N运动时，且始终保持MN=不变，当△MNP的面积最大时，请直接写出直线MN的表达式．

Answer 1

【答案】（1）y=x2+3x-4，C点坐标为（0，-4）；（2）E1（，），E2（-，-）；（3）y=x-4或y=-x-．

【解析】

试题分析：（1）根据待定系数法，可得函数解析式，根据自变量与函数值的对应关系，可得答案；

（2）根据勾股定理，可得BC的长，根据等角的正切值相等，可得HO的长，根据待定系数法，可得BE的解析式，根据解方程组，可得E点坐标；

（3）由题意△PMN是等腰直角三角形，得PM=PN=1，设M（a，a2+3a-4）则N（a+1，a2+3a+1）或（a+1，a2+3a-5），代入抛物线的解析式即可求解．

试题解析：（1）y=x2+bx+c，经过点B（-4，0）和点A（1，0），得

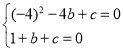，解得，

抛物线的解析式为y=x2+3x-4，

当x=0时，y=-4，

C点坐标为（0，-4）；

（2）如图：

由题意，得OB=OC=4，BC=4，

设l1与y轴交于点H，过A作AD⊥BC于点D，△ADB是等腰直角三角形，．

∵AD=BD=ABsin45°=，CD=，∠ACB=．

∵∠ACB=∠EBA，

∴HO=，H（0，），

设直线l1的解析式为y=kx+b，将B、C点坐标代入，得

k=，

l1的解析式为y=x+，

联立抛物线与l1，得x+=x2+3x-4，

解得x=，E1（，）；

同理l2：y=-x-，

-x-=x2+3x-4，

解得x=-，E2（-，-），

综上所述：E1（，），E2（-，-）；

（3）∵△PMN是直角三角形，斜边MN=，

∴当△PMN面积最大时，△PMN是等腰直角三角形，PM=PN=1，

由题意设M（a，a2+3a-4）则N（a+1，a2+3a-3）或（a+1，a2+3a-5），

∴a2+3a-3=（a+1）2+3（a+1）-4或a2+3a-5=（a+1）2+3（a+1）-4，

∴a=0或-．

①当a=0时，M（0，-4），N（1，-3），设直线MN为y=kx+b，则，解得，所以直线MN为y=x-4．

②当a=-时，M（-，-），N（-，-），

设直线MN为y=k′x+b′，则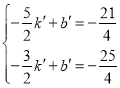解得，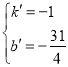

所以直线MN为y=-x-．