题目内容
直角三角形ABC的面积为120,且∠BAC=90°,AD是斜边上的中线,过D作DE⊥AB于E,连CE交AD于F,则△AFE的面积为
- A.18
- B.20
- C.22
- D.24
B
分析:根据已知及三角形中位线定理可求得ED= AC,AE=
AC,AE= AB,ED∥AC,根据相似三角形的判定可得到△DEF∽△ACF,从而不难求得几个三角形面积之间的关系,整理即可得到△AFE的面积.
AB,ED∥AC,根据相似三角形的判定可得到△DEF∽△ACF,从而不难求得几个三角形面积之间的关系,整理即可得到△AFE的面积.
解答: 解:∵∠BAC=90°,AD是斜边上的中线,过D作DE⊥AB于E,
解:∵∠BAC=90°,AD是斜边上的中线,过D作DE⊥AB于E,
∴ED= AC,AE=
AC,AE= AB,ED∥AC,
AB,ED∥AC,
∴S△ADE= =30,S△ACE=
=30,S△ACE= =60,△DEF∽△ACF,
=60,△DEF∽△ACF,
∴S△ADE:S△ACE=1:2,DE:AC=1:2,
∴S△DEF:S△ACF=1:4,
设S△DEF是t,S△AEF是xt,则S△ACF是4t,
∵S△ADE=S△DEF+S△AEF,S△ACE=S△ACF+S△AEF,
∵S△ADE:S△ACE=1:2,
∴2(t+xt)=xt+4t,
∴x=2,
∴2S△DEF=S△AEF,
∵S△ADE=30,
∴S△ACF=30× =20.
=20.
故选B.
点评:此题主要考查:(1)三角形中位线定理:三角形的中位线平行于第三边,并且等于第三边的一半.
(2)相似三角形的判定方法中的平行线法:平行于三角形的一边的直线与其他两边相交,所构成的三角形与原三角形相似.
分析:根据已知及三角形中位线定理可求得ED=
 AC,AE=
AC,AE= AB,ED∥AC,根据相似三角形的判定可得到△DEF∽△ACF,从而不难求得几个三角形面积之间的关系,整理即可得到△AFE的面积.
AB,ED∥AC,根据相似三角形的判定可得到△DEF∽△ACF,从而不难求得几个三角形面积之间的关系,整理即可得到△AFE的面积.解答:
 解:∵∠BAC=90°,AD是斜边上的中线,过D作DE⊥AB于E,
解:∵∠BAC=90°,AD是斜边上的中线,过D作DE⊥AB于E,∴ED=
 AC,AE=
AC,AE= AB,ED∥AC,
AB,ED∥AC,∴S△ADE=
 =30,S△ACE=
=30,S△ACE= =60,△DEF∽△ACF,
=60,△DEF∽△ACF,∴S△ADE:S△ACE=1:2,DE:AC=1:2,
∴S△DEF:S△ACF=1:4,
设S△DEF是t,S△AEF是xt,则S△ACF是4t,
∵S△ADE=S△DEF+S△AEF,S△ACE=S△ACF+S△AEF,
∵S△ADE:S△ACE=1:2,
∴2(t+xt)=xt+4t,
∴x=2,
∴2S△DEF=S△AEF,
∵S△ADE=30,
∴S△ACF=30×
 =20.
=20.故选B.
点评:此题主要考查:(1)三角形中位线定理:三角形的中位线平行于第三边,并且等于第三边的一半.
(2)相似三角形的判定方法中的平行线法:平行于三角形的一边的直线与其他两边相交,所构成的三角形与原三角形相似.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目
 如图,以等腰直角三角形ABC的斜边AB与边面内作等边△ABD,连接DC,以DC当边作等边△DCE,B、E在C、D的同侧,若AB=
如图,以等腰直角三角形ABC的斜边AB与边面内作等边△ABD,连接DC,以DC当边作等边△DCE,B、E在C、D的同侧,若AB=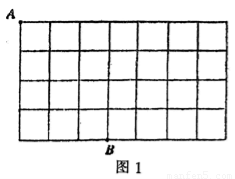

 如图,以等腰直角三角形ABC的斜边AB与边面内作等边△ABD,连接DC,以DC当边作等边△DCE,B、E在C、D的同侧,若AB=
如图,以等腰直角三角形ABC的斜边AB与边面内作等边△ABD,连接DC,以DC当边作等边△DCE,B、E在C、D的同侧,若AB= ,求BE的长.
,求BE的长.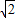 ,求BE的长.
,求BE的长.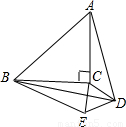
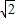 ,求BE的长.
,求BE的长.