题目内容
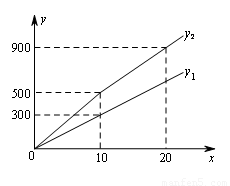
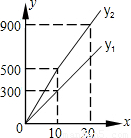
| 为发展旅游经济,我市某景区对门票采用灵活的售票方法吸引游客,门票定价为50 元/ 人,非节假日打a 折售票,节假日按团队人数分段定价售票,即m 人以下(含m 人)的团队接原价售票;超过m 人的团队,其中m 人仍按原价售票,超过m 人部分的游客打b 折售票,设某旅游团人数为x 人,非节假日购票款为y1(元),节假日购票款为y2(元),y1,y2与x之间的函数图象如图所示。 |
 |
| (1)观察图象可知:a=______ ;b=______ ;m=______ ; (2)直接写出y1,y2与x之间的函数关系式; (3)某旅行导游王娜于5 月1日带A 团,5 月20 日(非节假日)带B团都到该景区旅游,共付门票款1900元,A,B两个团队合计50 人,求A,B两个团队各有多少人? |
| 解:(1)a=6;b=8;m=10; (2)y1=30x;  ; ;(3)设A团有n人,则B团有(50-n)人 当0≤n≤10时,50n+30(50-n)=1900 解之得:n=20,这与n≤10矛盾 当n>10时,40n+100+30(50-n)=1900 解之得:n=30,50-30=20 答:A团有30人,B团有20人。 |

练习册系列答案
相关题目
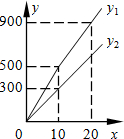 24、为发展旅游经济,我市某景区对门票釆用灵活的售票方法吸引游客.门票定价为50元/人,非节假日打a折售票,节假日按团队人数分段定价售票,即m人以下(含m人)的团队按原价售票;超过m人的团队,其中m人仍按原价售票,超过m人部分 的游客打b折售票.设某旅游团人数为x人,非节假日购票款为y1(元),节假日购票款为y2(元).y1与y2之间的函数图象如图所示.
24、为发展旅游经济,我市某景区对门票釆用灵活的售票方法吸引游客.门票定价为50元/人,非节假日打a折售票,节假日按团队人数分段定价售票,即m人以下(含m人)的团队按原价售票;超过m人的团队,其中m人仍按原价售票,超过m人部分 的游客打b折售票.设某旅游团人数为x人,非节假日购票款为y1(元),节假日购票款为y2(元).y1与y2之间的函数图象如图所示.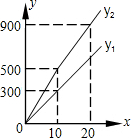 为发展旅游经济,我市某景区对门票釆用灵活的售票方法吸引游客.门票定价为50元/人,非节假日打a折售票,节假日按团队人数分段定价售票,即m人以下(含m人)的团队按原价售票;超过m人的团队,其中m人仍按原价售票,超过m人部分 的游客打b折售票.设某旅游团人数为x人,非节假日购票款为y1(元),节假日购票款为y2(元).y1与y2之间的函数图象如图所示.
为发展旅游经济,我市某景区对门票釆用灵活的售票方法吸引游客.门票定价为50元/人,非节假日打a折售票,节假日按团队人数分段定价售票,即m人以下(含m人)的团队按原价售票;超过m人的团队,其中m人仍按原价售票,超过m人部分 的游客打b折售票.设某旅游团人数为x人,非节假日购票款为y1(元),节假日购票款为y2(元).y1与y2之间的函数图象如图所示. (元),节假日购票款为
(元),节假日购票款为 (元).
(元).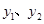 与x之间的函数图象如图所示.
与x之间的函数图象如图所示.
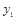 (元),节假日购票款为
(元),节假日购票款为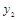 (元).
(元).