题目内容
(10分)如图,已知抛物线与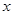 轴交于A(1,0),B(
轴交于A(1,0),B(![]() ,0)两点,与
,0)两点,与![]() 轴交于点
轴交于点
C(0,3),抛物线的顶点为P,连结AC.
(1)求此抛物线的解析式;
(2)在抛物线上找一点D,使得DC与AC垂直,且直线DC与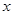 轴交于点Q,求点D的坐标;
轴交于点Q,求点D的坐标;
(3)抛物线对称轴上是否存在一点M,使得S△MAP=2S△ACP,若存在,求出M点坐标;若不存在,请说明理由.
(10分)解(1)设此抛物线的解析式为:
∵抛物线与![]() 轴交于A(1,0)、B(
轴交于A(1,0)、B( 两点,
两点,
∴![]()
又∵抛物线与![]() 轴交于点C(0,3)
轴交于点C(0,3)
∴![]() ,
,
∴![]()
∴![]()
即![]() ……………3分
……………3分
用其他解法参照给分
(2)∵点A(1,0),点C(0,3)
∴OA=1,OC=3,
∵DC⊥AC,OC⊥![]() 轴
轴
∴△QOC∽△COA
∴![]() ,即
,即![]()
∴OQ=9,……………………4分
又∵点Q在![]() 轴的负半轴上,∴Q(
轴的负半轴上,∴Q(
设直线DC的解析式为:![]() ,则
,则
![]() 解之得:
解之得:
∴直线DC的解析式为:![]() ……………………5分
……………………5分
∵点D是抛物线与直线DC的交点,
∴ 解之得:
解之得:
 (不合题意,应舍去)
(不合题意,应舍去)
∴点D(![]() ……………………6分
……………………6分
用其他解法参照给分
(3)如图,点M为直线 上一点,连结AM,PC,PA
上一点,连结AM,PC,PA
设点M(![]() ,直线
,直线![]() 与
与![]() 轴交于点E,∴AE=2
轴交于点E,∴AE=2
∵抛物线![]() 的顶点为P,对称轴为
的顶点为P,对称轴为
 ∴P(
∴P(
∴PE=4
则PM=![]()
∵S四边形AEPC=S四边形OEPC+S△AOC
=![]()
=
= ……………………7分
……………………7分
又∵S四边形AEPC= S△AEP+S△ACP
S△AEP=
∴+S△ACP=![]() ……………………8分
……………………8分
∵S△MAP=2S△ACP
∴![]()
∴![]()
∴![]() ,
,![]() ……………………9分
……………………9分
故抛物线的对称轴上存在点M使S△MAP=2S△ACP
点M(![]() 或
或![]() ……………………10分
……………………10分
用其他解法参照给分
解析:略

练习册系列答案
相关题目

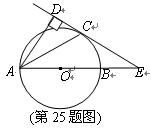
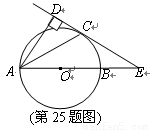
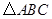 ,以
,以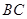 为直径,
为直径,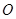 为圆心的半圆交
为圆心的半圆交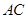 于点
于点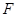 ,点
,点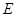 为弧CF的中点,连接
为弧CF的中点,连接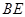 交
交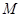 ,
,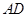 为△ABC的角平分线,且
为△ABC的角平分线,且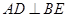 ,垂足为点
,垂足为点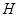 . [来源:]
. [来源:]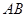 是半圆
是半圆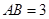 ,
,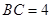 ,求
,求