题目内容
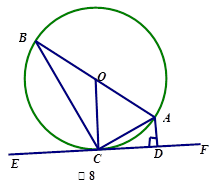
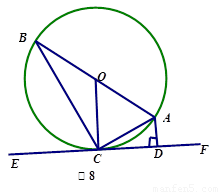
已知:如图8,AB是⊙O的直径,AC是弦,直线EF是过点C的⊙O的切线,AD⊥EF于点D.
1.求证:∠BAC=∠CAD
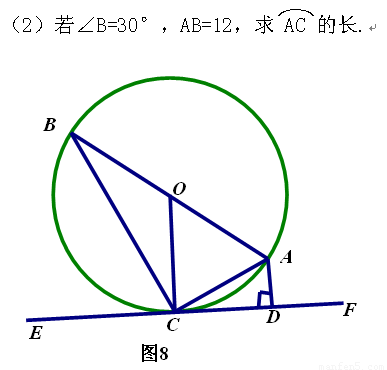
2.若∠B=30°,AB=12,求的长.
【答案】
1.证法一:连接OC
∵ EF是过点C的⊙O的切线。
∴ OC⊥EF 又AD⊥EF
∴ OC∥AD
∴ ∠OCA=∠CAD
又∵OA=OC
∴ ∠OCA=∠BAC
∴∠BAC=∠CAD
证法二:连接OC
∵ EF是过点C的⊙O的切线。
∴ OC⊥EF
∴∠OCA+∠ACD=90°
∵ AD⊥EF
∴ ∠CAD+∠ACD=90°
∴ ∠OCA=∠CAD
∵ OA=OC ,∴∠OCA=∠BAC
∴ ∠BAC=∠CAD
2.∵ ∠B=30° ∴∠AOC=60°
∵AB=12 ∴ 
∴l==2π
【解析】略

练习册系列答案
相关题目