题目内容
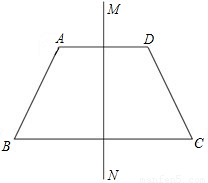
 如图,梯形中ABCD中,∠DBC=30°,DB=12
如图,梯形中ABCD中,∠DBC=30°,DB=12| 3 |
| 43 |
分析:此题可作辅助线:过D作DM∥AC,DM与BC的延长线交于点M,作DG⊥BM于G.则构造了一个平行四边形,且把梯形的面积转化为三角形的面积.根据平行四边形的性质,得对边相等.再根据30°所对的直角边是斜边的一半,求得DG的长.再根据勾股定理分别求得BG和MG的长.DG+MG即是梯形的上下底的和.进一步求其面积.
解答: 解:过D作DM∥AC,DM与BC的延长线交于点M,作DG⊥BM于G
解:过D作DM∥AC,DM与BC的延长线交于点M,作DG⊥BM于G
∵四边形ACMD为平行四边形
∴AD=CM,AC=DM
在Rt△DBG中,∠DBG=30°,DB=12
∴DG=6
,BG=18
在Rt△DGM中,GM=
=
=8
∴BM=BG+GM=26,又BM=BC+CM=BC+AD
∴EF=
(AD+BC)=
BM=13,
S梯形ABCD=
(AD+BC)×DG=
×26×6
=78
.
 解:过D作DM∥AC,DM与BC的延长线交于点M,作DG⊥BM于G
解:过D作DM∥AC,DM与BC的延长线交于点M,作DG⊥BM于G∵四边形ACMD为平行四边形
∴AD=CM,AC=DM
在Rt△DBG中,∠DBG=30°,DB=12
| 3 |
∴DG=6
| 3 |
在Rt△DGM中,GM=
| DM2-DG2 |
| 172-108 |
∴BM=BG+GM=26,又BM=BC+CM=BC+AD
∴EF=
| 1 |
| 2 |
| 1 |
| 2 |
S梯形ABCD=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
点评:注意梯形中又一条常见的辅助线:平移对角线.这条辅助线构造了一个平行四边形和一个由两条对角线和上下底的和组成的一个三角形.

练习册系列答案
相关题目
 如图:梯形中ABCD,AD∥BC,AB=CD=5,BC=6,∠C=60°,直线MN为梯形ABCD的对称轴,P为MN上一点,Q为CD上一点,那么PQ+CQ的最小值为
如图:梯形中ABCD,AD∥BC,AB=CD=5,BC=6,∠C=60°,直线MN为梯形ABCD的对称轴,P为MN上一点,Q为CD上一点,那么PQ+CQ的最小值为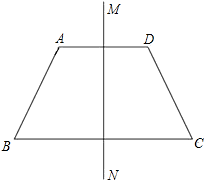 如图:梯形中ABCD,AD∥BC,AB=CD=5,BC=6,∠C=60°,直线MN为梯形ABCD的对称轴,P为MN上一点,Q为CD上一点,那么PQ+CQ的最小值为________.
如图:梯形中ABCD,AD∥BC,AB=CD=5,BC=6,∠C=60°,直线MN为梯形ABCD的对称轴,P为MN上一点,Q为CD上一点,那么PQ+CQ的最小值为________.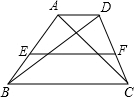 如图,梯形中ABCD中,∠DBC=30°,
如图,梯形中ABCD中,∠DBC=30°,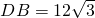 ,
,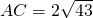 ,EF为梯形的中位线.求梯形的面积及EF的长.
,EF为梯形的中位线.求梯形的面积及EF的长.