题目内容
某单位的地板有三种边长相等的正多边形铺设，一个顶点处每种多边形只用一个，设这三种正多边形的边数分别是x，y，z．求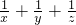
的值．
解：由题意可知：
+
+
=360°，
∴1-
+1-
+1-
=2，
∴
+
+
=
．
分析：这三种正多边形一个顶点处三个内角的度数之和正好等于360°．
点评：此题主要考查了平面镶嵌，解决本题的关键是理解多个多边形镶嵌的条件是：一个顶点处的内角和等于一个周角．
++=360°，∴1-
+1-+1-=2，∴
++=．分析：这三种正多边形一个顶点处三个内角的度数之和正好等于360°．
点评：此题主要考查了平面镶嵌，解决本题的关键是理解多个多边形镶嵌的条件是：一个顶点处的内角和等于一个周角．
练习册系列答案
心算口算巧算一课一练系列答案
应用题作业本系列答案
相关题目
的值．