题目内容
已知a= ,b=
,b=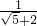 ;则
;则 的值是________.
的值是________.
20
分析:先把a、b分母有理化,然后得到a+b=2 ,ab=1;再把所求的分式通分变形得到原式=
,ab=1;再把所求的分式通分变形得到原式= ,然后把a+b=2
,然后把a+b=2 ,ab=1整体代入进行计算即可.
,ab=1整体代入进行计算即可.
解答:∵a= ,b=
,b=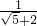 ,
,
∴a= +2,b=
+2,b= -2,
-2,
∴a+b=2 ,ab=1,
,ab=1,
原式= +2
+2
= +2
+2
= ,
,
∴当a+b=2 ,ab=1,
,ab=1,
原式=(2 )2=20.
)2=20.
故答案为20.
点评:本题考查了分式的化简求值:先把已知条件变形(分母有理化)得到两字母和与积的值,然后把所求的分式变形成这两字母和与积来表示的形式,再利用整体代入的方法代值进行计算.也考查了二次根式的化简求值.
分析:先把a、b分母有理化,然后得到a+b=2
 ,ab=1;再把所求的分式通分变形得到原式=
,ab=1;再把所求的分式通分变形得到原式= ,然后把a+b=2
,然后把a+b=2 ,ab=1整体代入进行计算即可.
,ab=1整体代入进行计算即可.解答:∵a=
 ,b=
,b=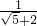 ,
,∴a=
 +2,b=
+2,b= -2,
-2,∴a+b=2
 ,ab=1,
,ab=1,原式=
 +2
+2=
 +2
+2=
 ,
,∴当a+b=2
 ,ab=1,
,ab=1,原式=(2
 )2=20.
)2=20.故答案为20.
点评:本题考查了分式的化简求值:先把已知条件变形(分母有理化)得到两字母和与积的值,然后把所求的分式变形成这两字母和与积来表示的形式,再利用整体代入的方法代值进行计算.也考查了二次根式的化简求值.

练习册系列答案
相关题目
 已知∠α,如图,则∠α的度数约为( )
已知∠α,如图,则∠α的度数约为( )| A、75° | B、60° | C、45° | D、30° |