题目内容
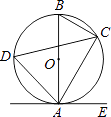
【题目】如图(1)在平面直角坐标系中,四边形OBCD是正方形,且D(0,2),点E是线段OB延长线上一点,M是线段OB上一动点(不包括O、B),做MN⊥DM,垂足为M,交∠CBE的平分线于点N.
(1)求点C的坐标;
(2)求证:MD=MN;
(3)如图(2),连接DN交BC于F,连接FM,探究线段MF、CF、OM之间有什么数量关系?并证明你的结论.
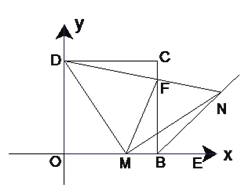
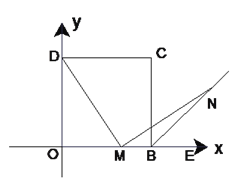
图(1) 图(2)
【答案】(1)C(2,2);(2)见解析(3)见解析
【解析】分析:(1)由正方形的性质可以得出OB=BC=OD就可以求出点C的坐标;
(2)在OD上取一点G,使OG=OM,就可以得出DG=BM,从而得出△GDM≌△BMN,就可以得出结论;
(3)由旋转可以得出△FCD≌△AOD,就可以得出OA=FC,∠ADM=∠CDM,进而得出△DMA≌△DMF,就可以得出AM=FM而得出结论.
详解:
(1)∵四边形OBCD是正方形,
∴OB=BC=OD,∠DOB=∠OBC=∠C=90°.
∵D(0,2),
∴OD=2,
∴OB=BC=OD=2,
∴C(2,2);
(2)在OD上取一点G,使OG=OM,
∴∠OGM=∠OMG=45°,
∴∠DGM=135°.
∵OD=OB,
∴OD-OG=OB-OM,
∴GD=BM.
∵MN⊥DM,
∴∠DMN=90°,
∴∠DMO+∠NMB=90°.
∵∠DMO+∠ODM=90°,
∴∠ODM=∠BMN.
∵BN平分∠CBE,
∴∠NBE=![]() ×90°=45°,
×90°=45°,
∴∠MBN=135°,
∴∠DGM=∠MBN.
在△GDM和△BMN中
 ,
,
∴△GDM≌△BMN(ASA),
∴MD=MN;
(3)OM+CF=MF

理由:∵MD=MN,∠DMN=90°,
∴∠MDN=45°,
∴∠ODM+∠FDC=45°.
∵△DCF绕点D顺时针旋转90°得△DOA,
∴△DCF≌△DOA,
∴AO=FC,∠ADO=∠FDC,AD=FD.
∴∠ADO+∠MDO=45°,
即∠ADM=45°.
∴∠ADM=∠CDM.
在△DMA和△DMF中
 ,
,
∴△DMA≌△DMF(SAS),
∴AM=FM.
∵AM=AO+MO,
∴AM=CF+MO,
∴OM+CF=MF.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】某自行车厂一周计划生产1 400辆自行车,平均每天生产200辆.由于各种原因,实际上每天的生产量与计划量相比有出入.表是某周的生产情况(增产为正,减产为负):
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
增减 | +5 | ﹣2 | ﹣4 | +13 | ﹣10 | +16 | ﹣9 |
(1)根据记录的数据可知该厂星期五生产自行车 辆;
(2)产量最多的一天比产量最少的一天多生产了 辆自行车;
(3)根据记录的数据可知该厂本周实际生产自行车 辆;
(4)该厂实行计件工资制,每生产一辆得60元,超额完成则每辆奖15元,少生产一辆则扣15元,那么该厂工人这一周的工资总额是多少?