题目内容
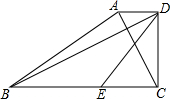 已知:如图,在梯形ABCD中,AD∥BC,AC⊥BD,AC=5,BD=12,若E是BC上的一点,BE=6.5,求DE的长.
已知:如图,在梯形ABCD中,AD∥BC,AC⊥BD,AC=5,BD=12,若E是BC上的一点,BE=6.5,求DE的长.
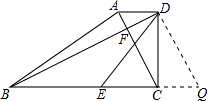 解:过D作DQ∥AC交BC的延长线于Q,
解:过D作DQ∥AC交BC的延长线于Q,∵AD∥BC,DQ∥AC,
∴四边形ACQD是平行四边形,
∴∠QDB=∠BFC=90°,DQ=AC=5,
由勾股定理得:BQ=
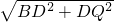 =13,
=13,∵BE=6.5,
∴EQ=6.5=BE,
∵DE是Rt△BDQ斜边BQ的中线,
∴DE=
 BQ=6.5,
BQ=6.5,答:DE的长是6.5.
分析:过D作DQ∥AC交BC的延长线于Q,得到平行四边形ACQD,推出∠QDB=∠BFC=90°,DQ=AC=5,由勾股定理求出BQ,推出BE=EQ,即可求出答案.
点评:本题主要考查对直角梯形,直角三角形斜边上中线的性质,勾股定理,平行四边形的性质和判定等知识点的理解和掌握,把直角梯形转化成平行四边形和直角三角形是解此题的关键.

练习册系列答案
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目
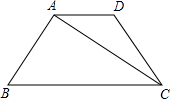 已知:如图,在梯形ABCD中,AD∥BC,AB=DC,∠D=120°,对角线CA平分∠BCD,且梯形的周长为20,求AC的长及梯形面积S.
已知:如图,在梯形ABCD中,AD∥BC,AB=DC,∠D=120°,对角线CA平分∠BCD,且梯形的周长为20,求AC的长及梯形面积S.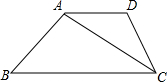 已知:如图,在梯形ABCD中,AD∥BC,∠B=45°,∠BAC=105°,AD=CD=4,
已知:如图,在梯形ABCD中,AD∥BC,∠B=45°,∠BAC=105°,AD=CD=4,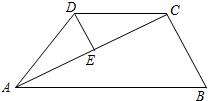 已知:如图,在梯形ABCD中,AB∥CD,AC⊥BC,AC平分∠DAB,点E为AC的中点.求证:DE=
已知:如图,在梯形ABCD中,AB∥CD,AC⊥BC,AC平分∠DAB,点E为AC的中点.求证:DE=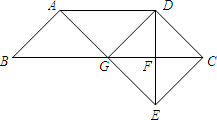 (2013•闵行区二模)已知:如图,在梯形ABCD中,AD∥BC,AB=CD,BC=2AD.DE⊥BC,垂足为点F,且F是DE的中点,联结AE,交边BC于点G.
(2013•闵行区二模)已知:如图,在梯形ABCD中,AD∥BC,AB=CD,BC=2AD.DE⊥BC,垂足为点F,且F是DE的中点,联结AE,交边BC于点G. 已知:如图,在梯形ABCD中,AD∥BC,CD=10cm,∠B=45度,∠C=30度,AD=5cm.
已知:如图,在梯形ABCD中,AD∥BC,CD=10cm,∠B=45度,∠C=30度,AD=5cm.