Question

【题目】如图，已知AB∥CD，∠B=40°，CN是∠BCE的平分线，CM⊥CN，求∠BCM的度数．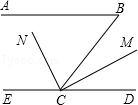

Answer 1

【答案】解：∵AB∥CD，∠B=40°， ∴∠BCE=180°﹣∠B=180°﹣40°=140°，
∵CN是∠BCE的平分线，
∴∠BCN= ∠BCE= ×140°=70°，
∵CM⊥CN，
∴∠BCM=20°
【解析】根据两直线平行，同旁内角互补求出∠BCE的度数，再根据角平分线的定义求出∠BCN的度数，然后再根据CM⊥CN即可求出∠BCM的度数．
【考点精析】本题主要考查了角的平分线和垂线的性质的相关知识点，需要掌握从一个角的顶点引出的一条射线，把这个角分成两个相等的角，这条射线叫做这个角的平分线；垂线的性质：1、过一点有且只有一条直线与己知直线垂直．2、垂线段最短才能正确解答此题．