Question

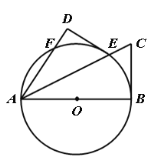
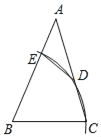
【题目】如图，在△ABC中．以点B为圆心，以BC为半径作弧，分别交AC、AB于点D，E，连接DE，若DE＝DC，AE＝4．AD＝5，则＝_____．

Answer 1

【答案】

【解析】

连接BD．先证明△BDE≌△BDC(SAS)，然后证明△AED∽△ADB，求出AB、BE，即可解决问题．

连接BD，

∵ED＝DC，

∴，

∴∠CBD＝∠DBE，

∵BE＝BD＝BC，

在△BDE和△BDC中

，

∴△BDE≌△BDC(SAS)，

∴∠BED＝∠BDE＝∠BDC＝∠BCD，

∵∠AED+∠BED＝180°，∠ADB+∠BDC＝180°，

∴∠AED＝∠ADB，

∵∠A＝∠A，

∴△AED∽△ADB，

∴，

∴，

∴AB＝，

∴BE＝AB﹣AE＝

∴S△AED：S△BED＝4：＝16：9，

∴S△ADE：S四边形BCDE＝16：18，

∴S△AED：S△ABC＝16：(16+18)＝8：17,

故答案为：．