题目内容
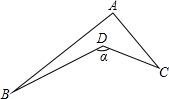如图，设∠BDC=∠α，则∠A，∠B，∠C与∠α的关系是________．
∠α=∠A+∠B+∠C
分析：延长BD交AC于点E．根据三角形的外角的性质即可求解．
解答：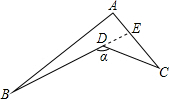
解：延长BD交AC于点E．
根据三角形的外角的性质，得
∠BDC=∠C+∠CED，∠CED=∠A+∠B，
∴∠α=∠A+∠B+∠C．
故答案为：∠α=∠A+∠B+∠C．
点评：此题注意构造三角形的外角，熟练运用三角形的外角等于和它不相邻的两个内角的和的性质．
分析：延长BD交AC于点E．根据三角形的外角的性质即可求解．
解答：
解：延长BD交AC于点E．根据三角形的外角的性质，得
∠BDC=∠C+∠CED，∠CED=∠A+∠B，
∴∠α=∠A+∠B+∠C．
故答案为：∠α=∠A+∠B+∠C．
点评：此题注意构造三角形的外角，熟练运用三角形的外角等于和它不相邻的两个内角的和的性质．
练习册系列答案
相关题目
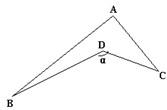12、如图，设∠BDC=∠α，则∠A，∠B，∠C与∠α的关系是
如图，在Rt△ABC中，∠ACB=90°，∠ABC=66°，将△ABC绕顶点C旋转到△A′B′C的位置，使顶点B恰好落在斜边A′B′上．设A′C与AB相交于点D，则∠BDC=（ ）
（2013•高要市二模）如图，在以O为圆心的两个同心圆中，小圆的半径为1，AB与小圆相切于点A，与大圆相交于B，大圆的弦BC⊥AB，过点C作大圆的切线交AB的延长线于D，OC交小圆于E．