Question

（2002•娄底）如图所示：点D、E在△ABC的AC边上，已知AD=CE，∠A=∠C，求证：∠ABD=∠CBE．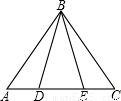

Answer 1

【答案】分析：由等角对等边得到，AB=BC，再由SAS得到△ABD≌△BCD得∠ABD=∠CBE．
解答：证明：∵∠A=∠C，
∴AB=CB．
在△ABD和△CBE中有，AB=BC，∠A=∠B，AD=CE，
∴△ABD≌△BCD．
∴∠ABD=∠CBE．
点评：本题考查了全等三角形的判定和性质；发现并利用△ABD≌△BCD是正确解答本题的关键．