题目内容
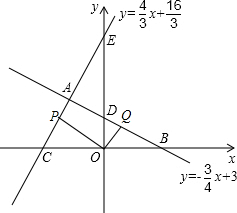
如图,已知一次函数y= x+3与函数y=
x+3与函数y= x+
x+ 的图象交于点A,且与x轴、y轴
的图象交于点A,且与x轴、y轴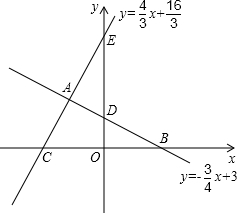 交于点B,点D,y=
交于点B,点D,y= x+
x+ 的图象与x轴、y轴交于点C,E,
的图象与x轴、y轴交于点C,E,
(1)求点C、点D、点A坐标;
(2)能否说明△ECO与△BDO相似吗?
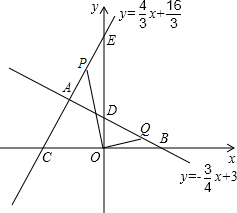
(3)动点P从点C出发沿射线CA以每秒4厘米的速度运动.同时,动点Q从点D出发沿射线DB运动,且始终保持OP⊥OQ.设运动时间为t秒(t>0).
①△PCO与△DQO相似吗?例说明理由;
②求动点Q的运动速度;
③设△APQ的面积为S(平方厘米),求S与t的函数关系式.
解:(1)∵y= x+
x+ 的图象与x轴交于点C,
的图象与x轴交于点C,
∴当y=0时, x+
x+ =0,解得x=-4,
=0,解得x=-4,
∴点C坐标为(-4,0);
∵一次函数y= x+3的图象与y轴
x+3的图象与y轴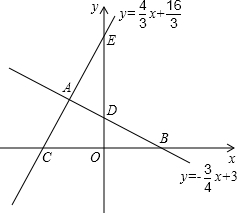 交于点D,
交于点D,
∴当x=0时,y=3,
∴点D坐标为(0,3);
解方程组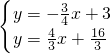 ,得
,得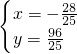 ,
,
∴A点坐标为(-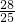 ,
, );
);
(2)△ECO与△BDO相似,理由如下:
∵y= x+3的图象与x轴交于点B,
x+3的图象与x轴交于点B,
∴当y=0时,x=4,
∴B点坐标为(4,0).
∵y= x+
x+ 的图象与y轴交于点E,
的图象与y轴交于点E,
∴E点坐标为(0, ).
).
在△ECO与△BDO中,
∵OE:OB= :4=4:3,OC:OD=4:3,
:4=4:3,OC:OD=4:3,
∴OE:OB=OC:OD,
又∵∠EOC=∠BOD=90°,
∴△ECO∽△BDO;
 (3)①△PCO与△DQO相似,理由如下:
(3)①△PCO与△DQO相似,理由如下:
∵∠COE=∠POQ=90°,
∴∠COE-∠POE=∠POQ-∠POE,
即∠COP=∠DOQ.
由(2)知△ECO∽△BDO,
∴∠PCO=∠QDO.
在△PCO与△QDO中,
∵∠COP=∠DOQ,∠PCO=∠QDO,
∴△PCO∽△QDO;
 ②∵△PCO∽△QDO,
②∵△PCO∽△QDO,
∴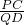 =
= ,
,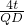 =
= ,
,
∴QD=3t,
∴动点Q的运动速度为每秒3厘米;
③分两种情况:
当0<t< 时,AP=AC-CP=
时,AP=AC-CP= -4t,AQ=AD+DQ=
-4t,AQ=AD+DQ= +3t,
+3t,
△APQ的面积为:S= AP•AQ=
AP•AQ= (
( -4t)(
-4t)( +3t)=-6t2+
+3t)=-6t2+ t+
t+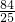 ;
;
当t≥ 时,AP=CP-AC=4t-
时,AP=CP-AC=4t- ,AQ=AD+DQ=
,AQ=AD+DQ= +3t,
+3t,
△APQ的面积为:S= AP•AQ=
AP•AQ= (4t-
(4t- )(
)( +3t)=6t2-
+3t)=6t2- t-
t-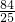 .
.
分析:(1)根据一次函数y= x+
x+ 的图象与x轴交于点C,可求点C坐标为(-4,0);根据一次函数y=
的图象与x轴交于点C,可求点C坐标为(-4,0);根据一次函数y= x+3的图象与y轴交于点D,可求点D坐标为(0,3);由于一次函数y=
x+3的图象与y轴交于点D,可求点D坐标为(0,3);由于一次函数y= x+3与函数y=
x+3与函数y= x+
x+ 的图象交于点A,联立这两个一次函数的解析式,得到关于x、y的二元一次方程组,解方程组即可求出A点坐标;
的图象交于点A,联立这两个一次函数的解析式,得到关于x、y的二元一次方程组,解方程组即可求出A点坐标;
(2)根据两边对应成比例,且夹角相等的两三角形相似即可得出△ECO∽△BDO;
(3)①根据两个角对应相等的两个三角形相似即可得出△PCO∽△QDO;
②根据△PCO∽△QDO,求得DQ的长,即点Q一秒移动的距离,即Q的速度;
②分别用时间t表示出AP,AQ的长,根据直角三角形的面积即可求得函数解析式.
点评:本题是一次函数的综合题,涉及到平面直角坐标系中求点的坐标,相似三角形的判定与性质,三角形的面积,注意(3)中,需根据P点的不同位置进行分类求解,这是解题的关键.
 x+
x+ 的图象与x轴交于点C,
的图象与x轴交于点C,∴当y=0时,
 x+
x+ =0,解得x=-4,
=0,解得x=-4,∴点C坐标为(-4,0);
∵一次函数y=
 x+3的图象与y轴
x+3的图象与y轴 交于点D,
交于点D,∴当x=0时,y=3,
∴点D坐标为(0,3);
解方程组
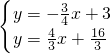 ,得
,得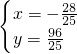 ,
,∴A点坐标为(-
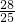 ,
, );
);(2)△ECO与△BDO相似,理由如下:
∵y=
 x+3的图象与x轴交于点B,
x+3的图象与x轴交于点B,∴当y=0时,x=4,
∴B点坐标为(4,0).
∵y=
 x+
x+ 的图象与y轴交于点E,
的图象与y轴交于点E,∴E点坐标为(0,
 ).
).在△ECO与△BDO中,
∵OE:OB=
 :4=4:3,OC:OD=4:3,
:4=4:3,OC:OD=4:3,∴OE:OB=OC:OD,
又∵∠EOC=∠BOD=90°,
∴△ECO∽△BDO;
 (3)①△PCO与△DQO相似,理由如下:
(3)①△PCO与△DQO相似,理由如下:∵∠COE=∠POQ=90°,
∴∠COE-∠POE=∠POQ-∠POE,
即∠COP=∠DOQ.
由(2)知△ECO∽△BDO,
∴∠PCO=∠QDO.
在△PCO与△QDO中,
∵∠COP=∠DOQ,∠PCO=∠QDO,
∴△PCO∽△QDO;
 ②∵△PCO∽△QDO,
②∵△PCO∽△QDO,∴
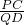 =
= ,
,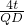 =
= ,
,∴QD=3t,
∴动点Q的运动速度为每秒3厘米;
③分两种情况:
当0<t<
 时,AP=AC-CP=
时,AP=AC-CP= -4t,AQ=AD+DQ=
-4t,AQ=AD+DQ= +3t,
+3t,△APQ的面积为:S=
 AP•AQ=
AP•AQ= (
( -4t)(
-4t)( +3t)=-6t2+
+3t)=-6t2+ t+
t+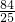 ;
;当t≥
 时,AP=CP-AC=4t-
时,AP=CP-AC=4t- ,AQ=AD+DQ=
,AQ=AD+DQ= +3t,
+3t,△APQ的面积为:S=
 AP•AQ=
AP•AQ= (4t-
(4t- )(
)( +3t)=6t2-
+3t)=6t2- t-
t-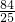 .
.分析:(1)根据一次函数y=
 x+
x+ 的图象与x轴交于点C,可求点C坐标为(-4,0);根据一次函数y=
的图象与x轴交于点C,可求点C坐标为(-4,0);根据一次函数y= x+3的图象与y轴交于点D,可求点D坐标为(0,3);由于一次函数y=
x+3的图象与y轴交于点D,可求点D坐标为(0,3);由于一次函数y= x+3与函数y=
x+3与函数y= x+
x+ 的图象交于点A,联立这两个一次函数的解析式,得到关于x、y的二元一次方程组,解方程组即可求出A点坐标;
的图象交于点A,联立这两个一次函数的解析式,得到关于x、y的二元一次方程组,解方程组即可求出A点坐标;(2)根据两边对应成比例,且夹角相等的两三角形相似即可得出△ECO∽△BDO;
(3)①根据两个角对应相等的两个三角形相似即可得出△PCO∽△QDO;
②根据△PCO∽△QDO,求得DQ的长,即点Q一秒移动的距离,即Q的速度;
②分别用时间t表示出AP,AQ的长,根据直角三角形的面积即可求得函数解析式.
点评:本题是一次函数的综合题,涉及到平面直角坐标系中求点的坐标,相似三角形的判定与性质,三角形的面积,注意(3)中,需根据P点的不同位置进行分类求解,这是解题的关键.

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目
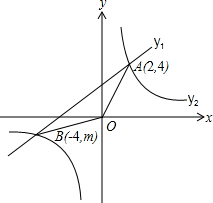 B(-4,m)两点.
B(-4,m)两点. 如图,已知一次函数y=kx+b的图象与反比例函数y=-
如图,已知一次函数y=kx+b的图象与反比例函数y=- (2013•新疆)如图,已知一次函数y1=kx+b与反比例函数
(2013•新疆)如图,已知一次函数y1=kx+b与反比例函数 如图,已知一次函数y=k1x+b经过A、B两点,将点A向上平移1个单位后刚好在反比例函数
如图,已知一次函数y=k1x+b经过A、B两点,将点A向上平移1个单位后刚好在反比例函数 如图,已知一次函数y=kx+b的图象交反比例函数
如图,已知一次函数y=kx+b的图象交反比例函数