题目内容
已知:如图,点C为线段AB上一点,△ACM, △CBN都是等边三角形,AN交MC于点E,BM交CN于点F.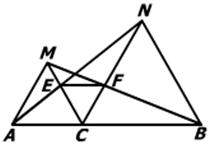
(1)求证:AN=BM;
(2)求证:△CEF为等边三角形
(1)证明略
(2)证明略解析:
证明(1):∵△ACM, △CBN是等边三角形
∴AC="MC,BC=NC," ∠ACM="60°," ∠NCB="60° " 2分
在△CAN和△MCB中
AC=MC,∠ACN=∠MCB,NC=" BC"
∴△CAN≌△MCB(SAS)
∴AN="BM " 5分
(2) ∵△CAN≌△MCB
∴∠CAN=∠MCB
又∵∠MCF=180°-∠ACM-∠NCB="180°-60°-60°=60°" 7分
∴∠MCF=∠ACE
在△CAE和△CMF中
∠CAE=∠CMF,CA=CM,∠ACE=∠MCF
∴△CAE≌△CMF(ASA) 10分
∴CE="CF"
∴△CEF为等腰三角形, 11分
又∵∠ECF="60°"
∴△CEF为等边三角形. 12分

练习册系列答案
 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案
相关题目
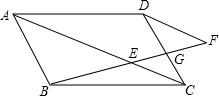
 26、已知:如图,点O为直线AB上一点,过点O在直线AB的同侧作射线OD、OC、OE,且OD是∠AOC的平分线,∠DOE=90°,请判断OE是否是∠BOC的平分线,并说明理由.
26、已知:如图,点O为直线AB上一点,过点O在直线AB的同侧作射线OD、OC、OE,且OD是∠AOC的平分线,∠DOE=90°,请判断OE是否是∠BOC的平分线,并说明理由.
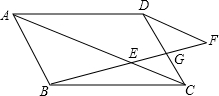
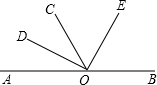 已知:如图,点O为直线AB上一点,过点O在直线AB的同侧作射线OD、OC、OE,且OD是∠AOC的平分线,∠DOE=90°,请判断OE是否是∠BOC的平分线,并说明理由.
已知:如图,点O为直线AB上一点,过点O在直线AB的同侧作射线OD、OC、OE,且OD是∠AOC的平分线,∠DOE=90°,请判断OE是否是∠BOC的平分线,并说明理由.