题目内容
一个圆内接正三角形面积为16| 3 |
分析：（1）利用三角形半径和边心距的关系，求出半径和边心距及三角形的高的比，根据比例设出边心距，再表示出三角形的高，即可列方程解答；（2）根据（1）的结论，结合直角三角形的性质求出AD的长，即可求出三角形的面积．
解答：解：（1）如图（1），
O为△ABC的中心，
AD为△ABC的边BC上的高，
则OD为边心距，
∴∠BAD=30°，
又∵AO=BO，
∴∠ABO=∠BAD=30°，
∴∠OBD=60°-30°=30°，
在Rt△OBD中，
BO=2DO，
即AO=2DO，
∴OD：OA：AD=1：2：3．
在正△ABC中，AD是高，设BD=x，则AD=BD•tan60°=
BD=
x．
∵正三角形ABC面积为16
cm2，
∴
BC•AD=16
，
∴
×2x•
x=16
，
∴x=4．
即BD=4，则AD=4
，
∵OD：OA：AD=1：2：3，
∴AO=4
×
=
cm．
即这个圆的半径为
cm．
（2）如图（2），
∵OD=
，∠OAD=30°，
∴AD=OD÷tan30°=
÷
=8，
∴S△ABC=6S△AOD=6×
×
×8=64
cm2．
O为△ABC的中心，
AD为△ABC的边BC上的高，
则OD为边心距，
∴∠BAD=30°，
又∵AO=BO，
∴∠ABO=∠BAD=30°，
∴∠OBD=60°-30°=30°，
在Rt△OBD中，
BO=2DO，
即AO=2DO，
∴OD：OA：AD=1：2：3．
在正△ABC中，AD是高，设BD=x，则AD=BD•tan60°=
| 3 |
| 3 |
∵正三角形ABC面积为16
| 3 |
∴
| 1 |
| 2 |
| 3 |
∴
| 1 |
| 2 |
| 3 |
| 3 |
∴x=4．
即BD=4，则AD=4
| 3 |
∵OD：OA：AD=1：2：3，
∴AO=4
| 3 |
| 2 |
| 3 |
8
| ||
| 3 |
即这个圆的半径为
8
| ||
| 3 |
（2）如图（2），
∵OD=
8
| ||
| 3 |
∴AD=OD÷tan30°=
8
| ||
| 3 |
| ||
| 3 |
∴S△ABC=6S△AOD=6×
| 1 |
| 2 |
8
| ||
| 3 |
| 3 |
点评：此题考查了圆的内接三角形和外切三角形，根据正三角形的性质和三角函数，求出半径和边心距的长是解题的关键．
练习册系列答案
阅读快车系列答案
相关题目
cm2，求（1）这个圆的半径；（2）这个圆的外切正三角形面积？
cm2，求（1）这个圆的半径；（2）这个圆的外切正三角形面积？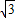
cm2,求(1)这个圆的半径；(2)这个圆的外切正三角形面积?