��Ŀ����
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�ֱ��l��y=��![]() x+4��y�ᡢx��ֱ���
x+4��y�ᡢx��ֱ���
E��F���߳�Ϊ2![]() �ĵȱ���ABC����BC��x���ϣ���������������x���������ƽ�ƣ���ƽ�ƹ����У��õ���A1B1C1������B1��ԭ���غ�ʱ������������⣺
�ĵȱ���ABC����BC��x���ϣ���������������x���������ƽ�ƣ���ƽ�ƹ����У��õ���A1B1C1������B1��ԭ���غ�ʱ������������⣺
��1�������A1�����꣬���жϵ�A1�Ƿ���ֱ��l�ϣ�
��2�������A1C1����ֱ�ߵĽ���ʽ��
��3��������ƽ������һ��P��ʹ����P��A1��C1��FΪ������ı�����ƽ���ı��Σ���ֱ��д��P�����꣮
���𰸡�(1)������;(2) y=��![]() x+6 ;(3) ��P������Ϊ��3
x+6 ;(3) ��P��������3![]() ��3����
��3����![]() ��3����5
��3����5![]() ����3����
����3����
��������
��1������A1��A1D��x���ڵ�D�����ݵȱ������ε����ʿɵó�B1D��A1D�ij��ȣ������ɵó���A1�����꣬������һ�κ���ͼ���ϵ�������������ҳ���A1��ֱ��l�ϣ�
��2���ɵȱ������εı߳����ҳ���C1�����꣬�ɵ�A1��C1�����꣬���ô���ϵ�������������A1C1����ֱ�ߵĽ���ʽ��
��3���ֱ�����A1C1F��������Ϊ�Խ����ҳ�ƽ���ı��Σ�����ƽ���ı��ε����ʼ����ҳ���P�����꣮
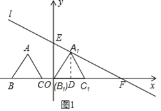
��1������A1��A1D��x���ڵ�D����ͼ1��ʾ��
�ߡ�A1B1C1�DZ߳�Ϊ2![]() �ĵȱ������Σ�
�ĵȱ������Σ�
��B1D=![]() ��2
��2![]() =
=![]() ��A1D=
��A1D=![]() ��2
��2![]() =3��
=3��
���A1��������![]() ��3����
��3����
�ߵ�x=![]() ʱ��y=��
ʱ��y=��![]() ��
��![]() +4=3��
+4=3��
���A1��ֱ��l�ϣ�
��2���ߡ�A1B1C1�DZ߳�Ϊ2![]() �ĵȱ������Σ�
�ĵȱ������Σ�
��B1C1=2![]() ��
��
���C1��������2![]() ��0����
��0����
���A1C1����ֱ�ߵĽ���ʽΪy=kx+b��k��0����
��A1��![]() ��3����C1��2
��3����C1��2![]() ��0������y=kx+b���ã�
��0������y=kx+b���ã�
![]() ����ã�
����ã�![]()
���A1C1����ֱ�ߵĽ���ʽΪy=��![]() x+6��
x+6��
��3����y=0ʱ���Щ�![]() x+4=0��
x+4=0��
��ã�x=4![]() ��
��
���F��������4![]() ��0����
��0����
������������ǣ���ͼ2����
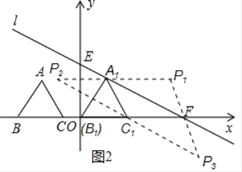
�ٵ�A1FΪ�Խ���ʱ���ı���A1C1FP1Ϊƽ���ı��Σ�
��A1��![]() ��3����C1��2
��3����C1��2![]() ��0����F��4
��0����F��4![]() ��0����
��0����
���P1��������![]() +4
+4![]() ��2
��2![]() ��3+0��0��������3
��3+0��0��������3![]() ��3����
��3����
�ڵ�A1C1Ϊ�Խ���ʱ���ı���A1P2C1FΪƽ���ı��Σ�
��A1��![]() ��3����C1��2
��3����C1��2![]() ��0����F��4
��0����F��4![]() ��0����
��0����
���P2��������![]() +2
+2![]() ��4
��4![]() ��3+0��0����������
��3+0��0����������![]() ��3����
��3����
�۵�C1FΪ�Խ���ʱ���ı���A1C1P3FΪƽ���ı��Σ�
��A1��![]() ��3����C1��2
��3����C1��2![]() ��0����F��4
��0����F��4![]() ��0����
��0����
���P3��������2![]() +4
+4![]() ��
��![]() ��0+0��3��������5
��0+0��3��������5![]() ����3����
����3����
������������P��������3![]() ��3����
��3����![]() ��3����5
��3����5![]() ����3����
����3����

 ��У����ϵ�д�
��У����ϵ�д�