题目内容
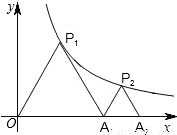
(2010•兰州)如图,P1是反比例函数y=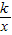 (k>0)在第一象限图象上的一点,点A1的坐标为(2,0).
(k>0)在第一象限图象上的一点,点A1的坐标为(2,0).(1)当点P1的横坐标逐渐增大时,△P1OA1的面积将如何变化?
(2)若△P1OA1与△P2A1A2均为等边三角形,求此反比例函数的解析式及A2点的坐标.
【答案】分析:(1)设P1(a,b),根据反比例函数的图象性质,可知y随x的增大而减小.又△P1OA1的面积= ×0A1×b=b.故当点P1的横坐标逐渐增大时,△P1OA1的面积将逐渐减小.
×0A1×b=b.故当点P1的横坐标逐渐增大时,△P1OA1的面积将逐渐减小.
(2)由于△P1OA1为等边三角形,作P1C⊥OA1,垂足为C,由等边三角形的性质及勾股定理可求出点P1的坐标,根据点P1是反比例函数y=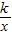 图象上的一点,利用待定系数法求出此反比例函数的解析式;作P2D⊥A1A2,垂足为D.设A1D=a,由于△P2A1A2为等边三角形,由等边三角形的性质及勾股定理,可用含a的代数式分别表示点P2的横、纵坐标,再代入反比例函数的解析式中,求出a的值,进而得出A2点的坐标.
图象上的一点,利用待定系数法求出此反比例函数的解析式;作P2D⊥A1A2,垂足为D.设A1D=a,由于△P2A1A2为等边三角形,由等边三角形的性质及勾股定理,可用含a的代数式分别表示点P2的横、纵坐标,再代入反比例函数的解析式中,求出a的值,进而得出A2点的坐标.
解答:解:(1)过P1作P1C⊥OA1,垂足为C,
设P1(a,b),
∵P1在第一象限,
∴△P1OA1的面积= ×0A1×b=b.
×0A1×b=b.
又∵当k>0时,在每一个象限内,y随x的增大而减小.
故当点P1的横坐标逐渐增大时,△P1OA1的面积将逐渐减小.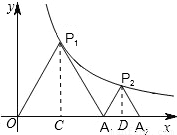
(2)因为△P1OA1为边长是2的等边三角形,
所以OC=1,P1C=2×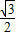 =
=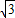 ,
,
所以P1(1,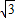 ).
).
代入y=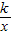 ,得k=
,得k=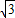 ,
,
所以反比例函数的解析式为y=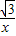 .
.
作P2D⊥A1A2,垂足为D.
设A1D=a,
则OD=2+a,P2D=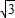 a,
a,
所以P2(2+a,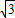 a).
a).
∵P2(2+a,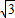 a)在反比例函数的图象上,
a)在反比例函数的图象上,
∴代入y=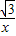 ,得(2+a)•
,得(2+a)•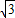 a=
a=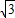 ,
,
化简得a2+2a-1=0
解得:a=-1±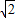 .
.
∵a>0,
∴a=-1+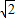 .∴A1A2=-2+2
.∴A1A2=-2+2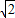 ,
,
∴OA2=OA1+A1A2=2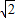 ,
,
所以点A2的坐标为(2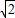 ,0).
,0).
点评:此题综合考查了反比例函数的性质,利用待定系数法求函数的解析式,正三角形的性质等多个知识点.此题难度稍大,综合性比较强,注意对各个知识点的灵活应用.
 ×0A1×b=b.故当点P1的横坐标逐渐增大时,△P1OA1的面积将逐渐减小.
×0A1×b=b.故当点P1的横坐标逐渐增大时,△P1OA1的面积将逐渐减小.(2)由于△P1OA1为等边三角形,作P1C⊥OA1,垂足为C,由等边三角形的性质及勾股定理可求出点P1的坐标,根据点P1是反比例函数y=
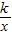 图象上的一点,利用待定系数法求出此反比例函数的解析式;作P2D⊥A1A2,垂足为D.设A1D=a,由于△P2A1A2为等边三角形,由等边三角形的性质及勾股定理,可用含a的代数式分别表示点P2的横、纵坐标,再代入反比例函数的解析式中,求出a的值,进而得出A2点的坐标.
图象上的一点,利用待定系数法求出此反比例函数的解析式;作P2D⊥A1A2,垂足为D.设A1D=a,由于△P2A1A2为等边三角形,由等边三角形的性质及勾股定理,可用含a的代数式分别表示点P2的横、纵坐标,再代入反比例函数的解析式中,求出a的值,进而得出A2点的坐标.解答:解:(1)过P1作P1C⊥OA1,垂足为C,
设P1(a,b),
∵P1在第一象限,
∴△P1OA1的面积=
 ×0A1×b=b.
×0A1×b=b.又∵当k>0时,在每一个象限内,y随x的增大而减小.
故当点P1的横坐标逐渐增大时,△P1OA1的面积将逐渐减小.

(2)因为△P1OA1为边长是2的等边三角形,
所以OC=1,P1C=2×
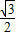 =
=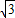 ,
,所以P1(1,
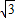 ).
).代入y=
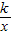 ,得k=
,得k=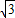 ,
,所以反比例函数的解析式为y=
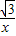 .
.作P2D⊥A1A2,垂足为D.
设A1D=a,
则OD=2+a,P2D=
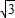 a,
a,所以P2(2+a,
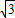 a).
a).∵P2(2+a,
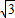 a)在反比例函数的图象上,
a)在反比例函数的图象上,∴代入y=
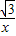 ,得(2+a)•
,得(2+a)•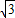 a=
a=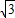 ,
,化简得a2+2a-1=0
解得:a=-1±
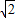 .
.∵a>0,
∴a=-1+
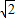 .∴A1A2=-2+2
.∴A1A2=-2+2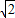 ,
,∴OA2=OA1+A1A2=2
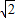 ,
,所以点A2的坐标为(2
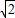 ,0).
,0).点评:此题综合考查了反比例函数的性质,利用待定系数法求函数的解析式,正三角形的性质等多个知识点.此题难度稍大,综合性比较强,注意对各个知识点的灵活应用.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目

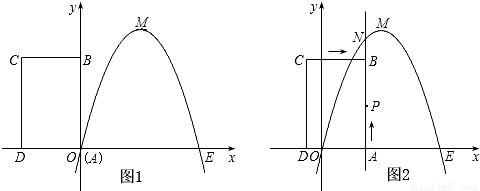
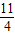 时,判断点P是否在直线ME上,并说明理由;
时,判断点P是否在直线ME上,并说明理由;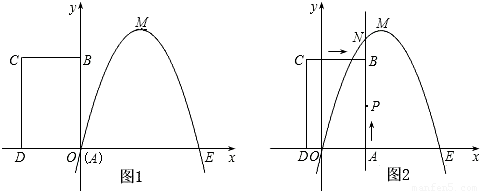
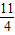 时,判断点P是否在直线ME上,并说明理由;
时,判断点P是否在直线ME上,并说明理由;