��Ŀ����
�� Rt��ABC �У���C��90�㣬BC��3cm��AC��4cm���Ե�C ΪԲ�ģ���2.5cm Ϊ�뾶��Բ�����C��ֱ��AB��λ�ù�ϵ�� ( )
A. �ཻ B. ���� C. ���� D. ����ȷ��
A �����������������Rt��ABC��,��C��90��,BC��3cm,AC��4cm,�������б��AB=5cm, �Ե�C ΪԲ��,��2.5cm Ϊ�뾶��Բ,��Բ��AB���е㣬BC>r�����ԡ�C ��ֱ��AB ��λ�ù�ϵ���ཻ.��ѡA.
��ϰ��ϵ�д�
�����Ŀ
���ٱ��չ�˾��һ�Ź���ij�������������IJ���ժ¼���£�
���� | ������������ | �ڸ�������������� |
40 | 80500 | 892 |
50 | 78009 | 951 |
60 | 69891 | 1200 |
70 | 45502 | 2119 |
80 | 16078 | 2001 |
�� | �� | �� |
�����ϱ������и��⣺
��1��ij�˽���50�꣬������ȥ���ĸ����Ƕ��٣����80��ĸ����Ƕ��٣�
������������Ч���֣�
��2�������20000��50����˲μ����ٱ��գ������������˾��⳥��Ϊ10��Ԫ��Ԥ�Ʊ��չ�˾�踶�⳥���ܶ�Ϊ���٣�
��1��0��0122��0��206��2��2438.18�� �����������������(1)����Ƶ�ʹ���.(2)����Ƶ�ʹ���20000�������ж�����ȥ�����ٳ����⳥��. ��������� ��1��P(50��ȥ��)= 0��0122,P���80�꣩=0��206 . ��2��951��78009��20000��10��2438.18��

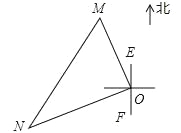

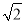 �� C. 4
�� C. 4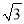 �� D. 8��
�� D. 8��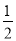 �ĸ����ǣ�������
�ĸ����ǣ�������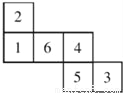
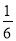 B.
B. 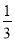 C.
C. 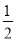 D.
D.