Question

如图，在平面坐标系中，点A、点B分别在x轴、y轴的正半轴上，且OA=OB，另有两点C(a,b)和D(b,-a)（a、b均大于0）；

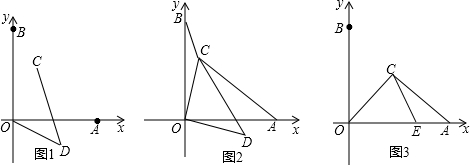
(1)连接OD、CD，求证：∠ODC=45⁰；
(2)连接CO、CB、CA，若CB=1，C0=2，CA=3，求∠OCB的度数；
(3)若a=b，在线段OA上有一点E，且AE=3，CE=5，AC=7，求⊿OCA 的面积。

Answer 1

(1)证明见解析；（2）135°；（3）.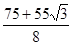

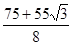试题分析：（1）过C点、D点向x轴、y轴作垂线，运用勾股定理计算，结合全等可证；
（2）连接DA，证△OCB≌△ODA（SAS），可得AD=CB=1，而OC=OD=2，故CD=2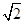，根据勾股定理逆定理可证∠ADC=90°，易得∠OCB=∠ODA=135°；
（3）作CF⊥OA，F为垂足，有CF²=CE²-EF²，CF²=CA²-AF²=CA²-（AE+EF）²，设EF=x，列出关于x的方程，求得x=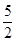，再在Rt△CEF中，根据勾股定理求得CF=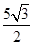，然后由三角形的面积公式即可求解．
试题解析：（1）证明：过C点、D点向x轴、y轴作垂线，垂足分别为M、N．

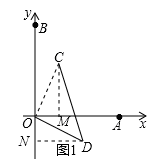
∵C（a，b），D（b，-a）（a、b均大于0），
∴OM=ON=a，CM=DN=b，
∴△OCM≌△ODN（SAS），
∴∠COM=∠DON．
∵∠DON+∠MOD=90°，
∴∠COM+∠MOD=90°，
∵OC=OD=，
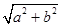∴△COD是等腰直角三角形，
∴∠ODC=45°；
（2）连接DA．

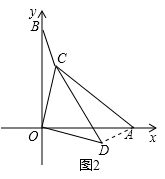
在△OCB与△ODA中，
，
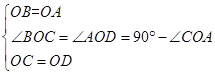∴△OCB≌△ODA（SAS），
∴AD=CB=1，∠OCB=∠ODA．
∵OC=OD=2，
∴CD=2．
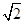∵AD²+CD²=1+8=9，AC²=9，
∴AD²+CD²=AC²，
∴∠ADC=90°，
∴∠OCB=∠ODA=90°+45°=135°；
（3）作CF⊥OA，F为垂足，由勾股定理得

CF²=CE²-EF²，CF²=CA²-AF²=CA²-（AE+EF）²，
设EF=x，可得5²-x²=7²-（3+x）²，
解得x=．
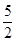在Rt△CEF中，得CF=，
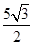∴OF=CF=，
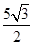∴△OCA的面积=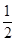•OA•CF==.
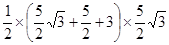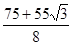考点: 1.勾股定理；2.全等三角形的判定与性质．