Question

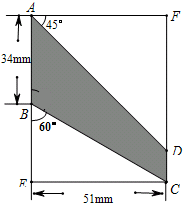（2013•甘井子区一模）在一个矩形材料中剪出中阴影所示的四边形（如图），请你根据图中的数据计算出BE、CD的长度（计算结果精确到0.1，参考数据：

3

≈1.73）．

Answer 1

分析：在Rt△BCE中，CE=51mm，∠EBC=60°，求得BE，在Rt△ADF中，由∠FAD=45°，从而求得DF=AF=51mm，从而求得BE，CD的长度．

解答：解：在Rt△BCE中，∵CE=51mm，∠EBC=60°，
∴tan60°=

EC

BE

，
∴BE=

51

tan60°

=

51

3

=17

3

≈29.4mm；
在Rt△ADF中，由∠FAD=45°，得∠ADF=∠DAF=45°，
因此DF=AF=51mm，
∴FC=AE≈34+29.4=63.4mm，
∴CD=FC-FD≈63.41-51=12.4mm，
因此BE的长度约为29.4mm，CD的长度约为12.4mm．

点评：本题考查了直角三角形的应用，考查了在直角三角形中利用特殊角的三角函数求得三角形的边．