题目内容
【题目】推理填空
如图，已知AB∥CD，∠A=∠C，试说明∠B=∠D．
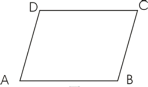
解：∵AB∥CD（已知）
∴∠B+∠C=180°（ ）
又∵∠A=∠C（已知）
∴∠B+________=180°（等量代换）
∴AD∥BC （ ）
∴∠C+∠D=180°（ ）
又∵∠B+∠C=180°（已证）
∴∠B=∠D （ ）
【答案】两直线平行，同旁内角互补；∠A；等量代换；同旁内角互补，两直线平行；两直线平行，同旁内角互补；同角的补角相等．
【解析】
根据平行线的性质（两直线平行，同旁内角互补）以及平行线的判定定理（同旁内角互补，两直线平行）填空．
∵AB∥DC，（已知）
∴∠B+∠C=180°，（两直线平行，同旁内角互补）
又∵∠A=∠C（已知），
∴∠B+∠A=180°，（等量代换），
∴AD∥BC，（同旁内角互补，两直线平行），
∴∠C+∠D=180°，（两直线平行，同旁内角互补），
又∵∠B+∠C=180°（已证）
∴∠B=∠D（同角的补角相等）．
练习册系列答案
相关题目
【题目】某公司在销售一种产品进价为10元的产品时，每年总支出为10万元（不含进价）．经过若干年销售得知，年销售量 
（万件）是销售单价 
（元）的一次函数，并得到如下部分数据：
销售单价 | 16 | 18[ | 20[ | 22 |
年销售量 | 5 | 4 | 3 | 2 |
（1）则 关于 的函数关系式是；
（2）写出该公司销售这种产品的年利润 
（万元）关于销售单价 （元）的函数关系式；当销售单价 为何值时，年利润最大?
（3）试通过（2）中的函数关系式及其大致图象，帮助该公司确定产品的销售单价范围，使年利润不低于14万元（请直接写出销售单价 的范围）．
