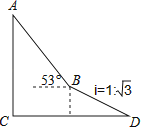��Ŀ����
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���OΪ����ԭ�㣬ֱ��l��������y=mx2+nx�ཻ��A��1��3 ![]() ����B��4��0�����㣮
����B��4��0�����㣮 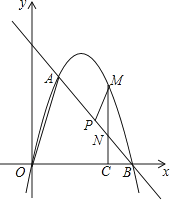
��1����������ߵĽ���ʽ��
��2�������������Ƿ���ڵ�D��ʹ�á�ABD�����߶�ABΪб�ߵ�ֱ�������Σ������ڣ������D�����ꣻ�������ڣ�˵�����ɣ�
��3����P���߶�AB��һ���㣬����P�����A��B�غϣ�������P��PM��OA������һ�����ڵ��������ڵ�M������M��MC��x���ڵ�C����AB�ڵ�N������BCN����PMN�����S��BCN��S��PMN����S��BCN=2S��PMN �� ��� ![]() ��ֵ���������ʱ��M�����꣮
��ֵ���������ʱ��M�����꣮
���𰸡�
��1��
�⣺��A��1��3 ![]() ����B��4��0����������y=mx2+nx��ͼ���ϣ�
����B��4��0����������y=mx2+nx��ͼ���ϣ�
�� ![]() �����
����� ![]() ��
��
�������߽���ʽΪy=�� ![]() x2+4
x2+4 ![]() x
x
��2��
�⣺�����������������⣬�������£�
����D��x����ʱ����ͼ1������A��AD��x���ڵ�D��

��A��1��3 ![]() ����
����
��D������1��0����
����D��y����ʱ����D��0��d������AD2=1+��3 ![]() ��d��2��BD2=42+d2����AB2=��4��1��2+��3
��d��2��BD2=42+d2����AB2=��4��1��2+��3 ![]() ��2=36��
��2=36��
�ߡ�ABD����ABΪб�ߵ�ֱ�������Σ�
��AD2+BD2=AB2����1+��3 ![]() ��d��2+42+d2=36�����d=
��d��2+42+d2=36�����d= ![]() ��
��
��D��������0�� ![]() ����0��
����0�� ![]() ����
����
���Ͽ�֪��������������D�㣬������Ϊ��1��0����0�� ![]() ����0��
����0�� ![]() ����
����
��3��
�⣺��ͼ2����P��PF��CM�ڵ�F��
��PM��OA��
��Rt��ADO��Rt��MFP��
�� ![]() =3
=3 ![]() ��
��
��MF=3 ![]() PF��
PF��
��Rt��ABD��BD=3��AD=3 ![]() ��
��
��tan��ABD= ![]() ��
��
���ABD=60�㣬��BC=a����CN= ![]() a��
a��
��Rt��PFN�У���PNF=��BNC=30�㣬
��tan��PNF= ![]() =
= ![]() ��
��
��FN= ![]() PF��
PF��
��MN=MF+FN=4 ![]() PF��
PF��
��S��BCN=2S��PMN��
�� ![]() a2=2��
a2=2�� ![]() ��4
��4 ![]() PF2��
PF2��
��a=2 ![]() PF��
PF��
��NC= ![]() a=2
a=2 ![]() PF��
PF��
�� ![]() =
= ![]() ��
��
��MN= ![]() NC=
NC= ![]() ��
�� ![]() a=
a= ![]() a��
a��
��MC=MN+NC=�� ![]() +
+ ![]() ��a��
��a��
��M��������4��a���� ![]() +
+ ![]() ��a����
��a����
��M�����������ϣ�����ɵé� ![]() ��4��a��2+4
��4��a��2+4 ![]() ��4��a��=��
��4��a��=�� ![]() +
+ ![]() ��a��
��a��
���a=3�� ![]() ��a=0����ȥ����
��a=0����ȥ����
OC=4��a= ![]() +1��MC=2
+1��MC=2 ![]() +
+ ![]() ��
��
���M�������� ![]() +1��2
+1��2 ![]() +
+ ![]() ����
����
����������1����A��B��������꣬���ô���ϵ��������������߽���ʽ��
����������2����D��x���Ϻ�y���ϣ���D��x����ʱ����A��AD��x�ᣬ����D��Ϊ����D����y����ʱ�����D������Ϊ��0��d�����ɷֱ��ʾ��AD��BD�������ù��ɶ����ɵõ�����d�ķ��̣������d��ֵ���Ӷ����������������D�����ꣻ
����������3����P��PF��CM�ڵ�F������Rt��ADO��Rt��MFP�Լ����Ǻ���������PF�ֱ��ʾ��MF��NF���Ӷ��ɱ�ʾ��MN����BC=a�������a��ʾ��CN��������S��BCN=2S��PMN �� ����PF��ʾ��a��ֵ���Ӷ�����PF��ʾ��CN������� ![]() ��ֵ������a�ɱ�ʾ��M������꣬���������߽���ʽ�����a��ֵ���Ӷ������M������꣮����Ϊ���κ������ۺ�Ӧ�ã��漰֪ʶ���д���ϵ���������ɶ��������������ε��ж������ʡ����뺯��ͼ��Ĺ�ϵ���������۵ȣ��ڣ�2����ע��ֵ�D��x���y��������������ڣ�3���зֱ�����PF��ʾ��MF��NC�ǽ���Ĺؼ���ע������������ƣ������漰֪ʶ��϶࣬�������ϴ��ۺ��Խ�ǿ���ر��ǵڣ�3���ʣ��ѶȺܴ�
��ֵ������a�ɱ�ʾ��M������꣬���������߽���ʽ�����a��ֵ���Ӷ������M������꣮����Ϊ���κ������ۺ�Ӧ�ã��漰֪ʶ���д���ϵ���������ɶ��������������ε��ж������ʡ����뺯��ͼ��Ĺ�ϵ���������۵ȣ��ڣ�2����ע��ֵ�D��x���y��������������ڣ�3���зֱ�����PF��ʾ��MF��NC�ǽ���Ĺؼ���ע������������ƣ������漰֪ʶ��϶࣬�������ϴ��ۺ��Խ�ǿ���ر��ǵڣ�3���ʣ��ѶȺܴ�