题目内容
如图,圆O经过平行四边形ABCD的三个顶点A、B、D,且圆心O在平行四边形ABCD的外部,tan∠DAB= ,
, ,圆O的半径为5,求平行四边形的面积.
,圆O的半径为5,求平行四边形的面积.
【答案】分析:根据垂径定理的推论,由已知得出OD⊥AB,AB=2AE,进而利用勾股定理得出DE,AB的长,即可求出平行四边形的面积.
解答: 解:连接OA,连接OD交AB于点E,
解:连接OA,连接OD交AB于点E,
∵ ,
,
∴OD⊥AB,AB=2AE,
在Rt△ADE中, ,
,
设DE=x,AE=2x,
则OE=5-x,
在Rt△AOE中,AO2=OE2+AE2,
∴52=(5-x)2+(2x)2,
解得:x1=2,x2=0(舍去),
∴DE=2,AB=2AE=8,
∴S平行四边形ABCD=8×2=16,
即平行四边形ABCD的面积为16.
点评:此题主要考查了垂径定理的推论以及勾股定理和平行四边形的面积求法等知识,根据已知得出AO2=OE2+AE2是解题关键.
解答:
 解:连接OA,连接OD交AB于点E,
解:连接OA,连接OD交AB于点E,∵
 ,
,∴OD⊥AB,AB=2AE,
在Rt△ADE中,
 ,
,设DE=x,AE=2x,
则OE=5-x,
在Rt△AOE中,AO2=OE2+AE2,
∴52=(5-x)2+(2x)2,
解得:x1=2,x2=0(舍去),
∴DE=2,AB=2AE=8,
∴S平行四边形ABCD=8×2=16,
即平行四边形ABCD的面积为16.
点评:此题主要考查了垂径定理的推论以及勾股定理和平行四边形的面积求法等知识,根据已知得出AO2=OE2+AE2是解题关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
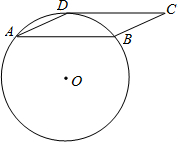 如图,圆O经过平行四边形ABCD的三个顶点A、B、D,且圆心O在平行四边形ABCD的外部,tan∠DAB=
如图,圆O经过平行四边形ABCD的三个顶点A、B、D,且圆心O在平行四边形ABCD的外部,tan∠DAB= (2012•虹口区二模)如图,圆O经过平行四边形ABCD的三个顶点A、B、D,且圆心O在平行四边形ABCD的外部,tan∠DAB=
(2012•虹口区二模)如图,圆O经过平行四边形ABCD的三个顶点A、B、D,且圆心O在平行四边形ABCD的外部,tan∠DAB=
 如图,圆O经过平行四边形ABCD的三个顶点A、B、D,且圆心O在平行四边形ABCD的外部,tan∠DAB=
如图,圆O经过平行四边形ABCD的三个顶点A、B、D,且圆心O在平行四边形ABCD的外部,tan∠DAB= ,D为弧AB的中点,⊙O的半径为5,求平行四边形的面积.
,D为弧AB的中点,⊙O的半径为5,求平行四边形的面积. 如图,圆O经过平行四边形ABCD的三个顶点A、B、D,且圆心O在平行四边形ABCD的外部,tan∠DAB=
如图,圆O经过平行四边形ABCD的三个顶点A、B、D,且圆心O在平行四边形ABCD的外部,tan∠DAB= ,圆O的半径为5,求平行四边形的面积.
,圆O的半径为5,求平行四边形的面积.