题目内容
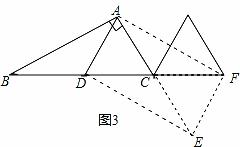
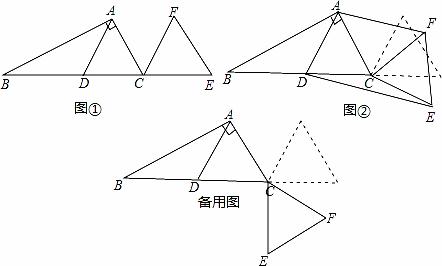
在Rt△ABC中,∠BAC=90°,∠B=30°,线段AD是BC边上的中线,如图①,将△ADC沿直线BC平移,使点D与点C重合,得到△FCE;如图②,再将△FCE绕点C顺时针旋转,设旋转角为α(0°<α≤90°),连接AF、DE.
(1)在旋转过程中,当∠ACE=150°时,求旋转角α的度数;
(2)请探究在旋转过程中,四边形ADEF能形成那些特殊四边形?请说明理由.








24.
解:(1)在图①中,∵∠BAC=90°,∠B=30°,
∴∠ACE=∠BAC+∠B=120°.
在旋转过程中,分两种情况:
①当点E和点D在直线AC两侧时,如图2,
∵∠ACE=150°,
∴α=150°﹣120°=30°;
②当点E和点D在直线AC的同侧时,如备用图,
∵∠ACB=180°﹣∠BAC﹣∠B=60°,
∴∠DCE=∠ACE﹣∠ACB=150°﹣60°=90°,
∴α=180°﹣∠DCE=90°.
∴旋转角α为30°或90°;
(2)四边形ADEF能形成等腰梯形和矩形.
∵∠BAC=90°,∠B=30°,![]() ,
,
又AD是BC边上的中线,∴AD=CD=![]() BC=AC,
BC=AC,
∴△ADC为正三角形.
①当α=60°时,∠ACE=120°+60°=180°,
∵CA=CE=CD=CF,∴四边形ADEF为平行四边形,
又∵AE=DF,∴四边形ADEF为矩形,
②当α≠60°时,∠ACF≠120°,∠DCE=360°﹣60°﹣60°﹣∠ACF≠120°,
显然DE≠AF,
∵AC=CF,CD=CE
∵2∠FAC+∠ACF=180°,2∠CDE+∠DCE=180°∠ACF+∠DCE=360°﹣60°﹣60°=240°,
∴2∠FAC+2∠CDE=120°,
∴∠FAC+∠CDE=60°,
∵∠DAF+∠ADE=120°+60°=180°
∴AF∥DE.
∴四边形ADEF为等腰梯形.

 阅读快车系列答案
阅读快车系列答案| A、asinA | ||
B、
| ||
| C、acosA | ||
D、
|
 如图,在Rt△ABC中,∠C=90°,CD⊥AB于D,且AD:BD=9:4,则AC:BC的值为( )
如图,在Rt△ABC中,∠C=90°,CD⊥AB于D,且AD:BD=9:4,则AC:BC的值为( )| A、9:4 | B、9:2 | C、3:4 | D、3:2 |
 已知:如图,在Rt△ABC中,∠C=90°,AC=12,BC=9,D是AB上一点,以BD为直径的⊙O切AC于E,求⊙O的半径.
已知:如图,在Rt△ABC中,∠C=90°,AC=12,BC=9,D是AB上一点,以BD为直径的⊙O切AC于E,求⊙O的半径. 如图,已知:在Rt△ABC中,∠C=90°,AB=12,点D是AB的中点,点O是△ABC的重心,则OD的长为( )
如图,已知:在Rt△ABC中,∠C=90°,AB=12,点D是AB的中点,点O是△ABC的重心,则OD的长为( )