Question

【题目】若两个二次函数图象的顶点相同，开口大小相同，但开口方向相反，则称这两个二次函数为“对称二次函数”．

(1)请写出二次函数y＝2(x－2)2＋1的“对称二次函数”；

(2)已知关于x的二次函数y1＝x2－3x＋1和y2＝ax2＋bx＋c，若y1－y2与y1互为“对称二次函数”，求函数y2的表达式，并求出当－3≤x≤3时，y2的最大值．

Answer 1

【答案】(1) y＝－2(x－2)2＋1；

(2) .

【解析】

（1）根据“对称二次函数”的定义即可求解；
（2）根据y1-y2与y1互为“对称二次函数”，求出函数y2的表达式，然后将函数y2的表达式转化为顶点式，再利用二次函数的性质就可以解决问题．

(1)二次函数y＝2(x－2)2＋1的“对称二次函数”是y＝－2(x－2)2＋1；

(2)∵y1＝x2－3x＋1，y2＝ax2＋bx＋c，

∴y1－y2＝(1－a)x2－(3＋b)x＋1－c＝(1－a)·[x－]＋.

又y1－y2与y1互为“对称二次函数”，y1＝x2－3x＋1＝(x－)2－，

∴解得

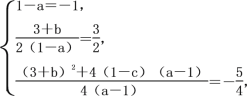∴y2＝2x2－6x＋，

∴y2＝2(x－)2，

∴y2的对称轴为直线x＝，

∵2＞0，且－3≤x≤3，

∴当x＝－3时，y2最大值＝2×(－3)2－6×(－3)＋＝.