题目内容
已知二次函数y=ax2+bx+c(a≠0)的图象向左平移2个单位,向下平移1个单位后得到二次函数y=x2+2x的图象,则二次函数y=ax2+bx+c(a≠0)的解析式为________.
y=x2-2x+1
分析:利用抛物线和二次函数图象的性质.
解答:可从新抛物线上找3个点(0,0),(1,3),(-1,-1).向右平移2个单位,向上平移1个单位得(2,1)(3,4)(1,0).则这三点符合原抛物线的解析式.那么4a+2b+c=1,9a+3b+c=4,a+b+c=0,解得:a=1,b=-2,c=1.故解析式为:y=x2-2x+1.
点评:原抛物线上有三个未知数,所以从原抛物线上找三个点是解决问题的关键,这三个点是新抛物线上的经过平移转换还原的三个点.
分析:利用抛物线和二次函数图象的性质.
解答:可从新抛物线上找3个点(0,0),(1,3),(-1,-1).向右平移2个单位,向上平移1个单位得(2,1)(3,4)(1,0).则这三点符合原抛物线的解析式.那么4a+2b+c=1,9a+3b+c=4,a+b+c=0,解得:a=1,b=-2,c=1.故解析式为:y=x2-2x+1.
点评:原抛物线上有三个未知数,所以从原抛物线上找三个点是解决问题的关键,这三个点是新抛物线上的经过平移转换还原的三个点.

练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目
已知二次函数y=ax+bx+c(a≠0,a,b,c为常数),对称轴为直线x=1,它的部分自变量与函数值y的对应值如下表,写出方程ax2+bx+c=0的一个正数解的近似值________(精确到0.1).
| x | -0.1 | -0.2 | -0.3 | -0.4 |
| y=ax2+bx+c | -0.58 | -0.12 | 0.38 | 0.92 |
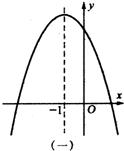 21、已知二次函数y=a(x+1)2+c的图象如图所示,则函数y=ax+c的图象只可能是( )
21、已知二次函数y=a(x+1)2+c的图象如图所示,则函数y=ax+c的图象只可能是( )
