题目内容
如图，矩形ABCD沿AE折叠，使D点恰好落在边BC上的点F处，若AB=8，AD=10，则EF=（ ）| A、3 | B、4 | C、5 | D、6 |
分析：先根据翻折变换的性质得出DE=FE，AD=AF，在△ABF中利用勾股定理可求出BF的长，同理，△CEF中，设EF=DE=x，利用勾股定理求出x的值即可．
解答：解：根据翻折不变性可知，
DE=FE，AD=AF，∠AFE=∠ADE．
在△ABF中，
AB=8，AF=AD=10，
根据勾股定理BF=
=
=6；
设EF=DE=x，则EC=8-x，
在△CEF中，EF2=EC2+CF2，
即x2=（8-x）2+（10-6）2，
解得x=5．
故选C．
DE=FE，AD=AF，∠AFE=∠ADE．
在△ABF中，
AB=8，AF=AD=10，
根据勾股定理BF=
| AF2-AB2 |
| 102-82 |
设EF=DE=x，则EC=8-x，
在△CEF中，EF2=EC2+CF2，
即x2=（8-x）2+（10-6）2，
解得x=5．
故选C．
点评：本题考查的是图形翻折变换的性质，即折叠是一种对称变换，它属于轴对称，折叠前后图形的形状和大小不变，位置变化，对应边和对应角相等．
练习册系列答案
快捷英语周周练系列答案
相关题目
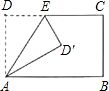如图将矩形ABCD沿AE折叠，得到如图所示的图形，已知∠CED′=55°，则∠BAD′的大小是
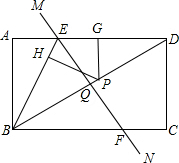如图，矩形ABCD沿直线MN折叠，使点D落在点B处，点E、F分别是边AD、BC与MN的交点，Q是MM与对角线BD的交点，P是对角线BD上任意一点，PH⊥BE于H，PG⊥AD于G．
如图，矩形ABCD沿∠A的三等分线经两次折叠后，四边形CDEF的面积为（ ）| A、10 | ||
B、20
| ||
C、10
| ||
D、10
|
（2010•邢台一模）如图，矩形ABCD沿EF折叠，点B恰好落在点D上，若AB=4cm，BC=8cm，则阴影部分的面积为