题目内容
（2003•海南）如图，在菱形ABCD中，AE⊥BC于E，已知EC=1，cosB=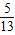
，则这个菱形的面积是 ．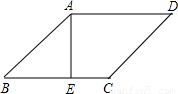
【答案】分析：解直角三角形ABE，求出AB、AE后计算．
解答：
解：设菱形的边长为x，
则BE的长为x-1．
∵cosB=
，
∴
=
=
，
可得：x=
，
∴BE=
，
∵AB2=BE2+AE2，即
=
+AE2，
∴AE=
．
故：S菱形=BC×AE=
×
=
．
点评：本题主要是根据三角函数和菱形的特殊性质可求出菱形的边及高，代入菱形的面积即可求出．
解答：
解：设菱形的边长为x，则BE的长为x-1．
∵cosB=
，∴
==，可得：x=
，∴BE=
，∵AB2=BE2+AE2，即
=+AE2，∴AE=
．故：S菱形=BC×AE=
×=．点评：本题主要是根据三角函数和菱形的特殊性质可求出菱形的边及高，代入菱形的面积即可求出．
练习册系列答案
同步练习河南大学出版社系列答案
同步练习西南师范大学出版社系列答案
补充习题江苏系列答案
学练快车道口算心算速算天天练系列答案
相关题目
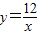的图象与一次函数y=kx+4的图象相交于P、Q两点，并且P点的纵坐标是6．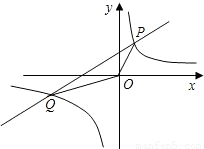
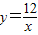的图象与一次函数y=kx+4的图象相交于P、Q两点，并且P点的纵坐标是6．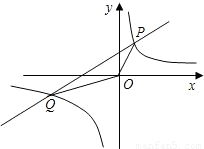
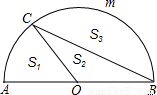
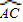为半圆的
．设扇形AOC、△COB、弓形BmC的面积分别为S1、S2、S3，则下列结论正确的是（ ）
