题目内容
(2009•石景山区二模)如图,四边形ABCD是菱形,点D的坐标是(0,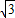 ),以点C为顶点的抛物线y=ax2+bx+c恰经过x轴上的点A,B.
),以点C为顶点的抛物线y=ax2+bx+c恰经过x轴上的点A,B.(1)求点C的坐标;
(2)若抛物线向上平移后恰好经过点D,求平移后抛物线的解析式.

【答案】分析:(1)连接AC,在菱形ABCD中,CD∥AB,AB=BC=CD=DA,由抛物线对称性可知AC=BC.∴△ABC,△ACD都是等边三角形.可求CD=AD= =2,可得点C的坐标为(2,
=2,可得点C的坐标为(2,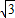 ).
).
(2)由抛物线y=ax2+bx+c的顶点为(2,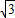 ),可设抛物线的解析式为:y=a
),可设抛物线的解析式为:y=a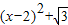
由(1)可得A(1,0),把A(1,0)代入上式,解得a=-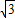 ,设平移后抛物线的解析式为y=-
,设平移后抛物线的解析式为y=-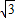 (x-2)2+k,把(0,
(x-2)2+k,把(0,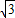 )代入上式得K=5
)代入上式得K=5 .即可得到平移后抛物线的解析式.
.即可得到平移后抛物线的解析式.
解答: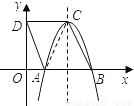 解:(1)连接AC,在菱形ABCD中,CD∥AB,
解:(1)连接AC,在菱形ABCD中,CD∥AB,
AB=BC=CD=DA,
由抛物线对称性可知AC=BC.(1分)
∴△ABC,△ACD都是等边三角形.
∴CD=AD=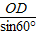 =2(2分)
=2(2分)
∴点C的坐标为(2,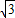 ).(3分)
).(3分)
(2)由抛物线y=ax2+bx+c的顶点为(2,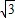 ),
),
可设抛物线的解析式为.y=a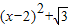
由(1)可得A(1,0),把A(1,0)代入上式,
解得a=-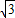 .(5分)
.(5分)
设平移后抛物线的解析式为y=-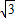 (x-2)2+k,
(x-2)2+k,
把(0,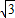 )代入上式得K=5
)代入上式得K=5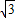 .
.
∴平移后抛物线的解析式为:
y=-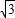 (x-2)2+5
(x-2)2+5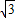 (7分)
(7分)
即y=-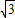 x2+4
x2+4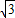 x+
x+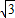 .
.
点评:抛物线平移问题,实际上就是两条抛物线顶点之间的问题,找到了顶点的变化就知道了抛物线的变化,由此看来,只要抓住事物本质的东西,问题就可以迎刃而解了.
 =2,可得点C的坐标为(2,
=2,可得点C的坐标为(2,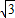 ).
).(2)由抛物线y=ax2+bx+c的顶点为(2,
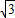 ),可设抛物线的解析式为:y=a
),可设抛物线的解析式为:y=a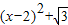
由(1)可得A(1,0),把A(1,0)代入上式,解得a=-
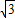 ,设平移后抛物线的解析式为y=-
,设平移后抛物线的解析式为y=-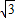 (x-2)2+k,把(0,
(x-2)2+k,把(0,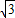 )代入上式得K=5
)代入上式得K=5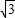 .即可得到平移后抛物线的解析式.
.即可得到平移后抛物线的解析式.解答:
 解:(1)连接AC,在菱形ABCD中,CD∥AB,
解:(1)连接AC,在菱形ABCD中,CD∥AB,AB=BC=CD=DA,
由抛物线对称性可知AC=BC.(1分)
∴△ABC,△ACD都是等边三角形.
∴CD=AD=
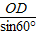 =2(2分)
=2(2分)∴点C的坐标为(2,
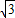 ).(3分)
).(3分)(2)由抛物线y=ax2+bx+c的顶点为(2,
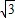 ),
),可设抛物线的解析式为.y=a
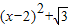
由(1)可得A(1,0),把A(1,0)代入上式,
解得a=-
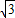 .(5分)
.(5分)设平移后抛物线的解析式为y=-
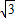 (x-2)2+k,
(x-2)2+k,把(0,
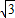 )代入上式得K=5
)代入上式得K=5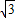 .
.∴平移后抛物线的解析式为:
y=-
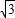 (x-2)2+5
(x-2)2+5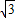 (7分)
(7分)即y=-
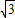 x2+4
x2+4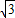 x+
x+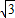 .
.点评:抛物线平移问题,实际上就是两条抛物线顶点之间的问题,找到了顶点的变化就知道了抛物线的变化,由此看来,只要抓住事物本质的东西,问题就可以迎刃而解了.

练习册系列答案
 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案
相关题目

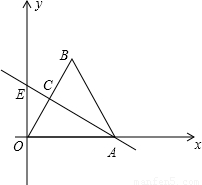
 ,0),点B在第一象限,AC是∠OAB的平分线,并且与y轴交于点E,点M为直线AC上一个动点,把△AOM绕点A顺时针旋转,使边AO与边AB重合,得到△ABD.
,0),点B在第一象限,AC是∠OAB的平分线,并且与y轴交于点E,点M为直线AC上一个动点,把△AOM绕点A顺时针旋转,使边AO与边AB重合,得到△ABD. ?若存在,求出点M的坐标;若不存在,请说明理由.
?若存在,求出点M的坐标;若不存在,请说明理由.