题目内容
如图，梯形ABCD中，AD∥BC，E、F分别是AB、CD上的点，且EF∥BC，| AE |
| BE |
| BC |
| AD |
| 5 |
| 3 |
| AB |
| a |
| DC |
| b |
| EF |
| a |
| b |
考点：*平面向量
专题：
分析：过点A作AH∥CD交EF于G，交BC于H，可得AD=GF=CH，然后用BH表示出CH，再求出
，根据相似三角形对应边成比例可得
=
，再用BH表示出EG，然后表示出EF，再根据向量的三角形法则求出BH，即可得解．
| AE |
| AB |
| AE |
| AB |
| EG |
| BH |
解答：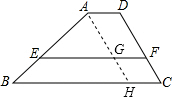
解：如图，过点A作AH∥CD交EF于G，交BC于H，
∵AD∥BC，EF∥BC，
∴AD=GF=CH，
∵
=
，
∴BC=
AD，
∴BH=BC-CH=
AD-AD=
AD=
CH，
∴CH=
BH，
∵
=
，
∴
=
，
∵EF∥BC，
∴△AEG∽△ABH，
∴
=
=
，
∴EG=
BH，
∴EF=EG+GF=
BH+
BH=
BH，
∵
=
，
=
，
∴
=
-
=
-
，
∴
=
（
-
）．
故答案为：
（
-
）．
解：如图，过点A作AH∥CD交EF于G，交BC于H，∵AD∥BC，EF∥BC，
∴AD=GF=CH，
∵
| BC |
| AD |
| 5 |
| 3 |
∴BC=
| 5 |
| 3 |
∴BH=BC-CH=
| 5 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
∴CH=
| 3 |
| 2 |
∵
| AE |
| BE |
| 5 |
| 3 |
∴
| AE |
| AB |
| 5 |
| 8 |
∵EF∥BC，
∴△AEG∽△ABH，
∴
| AE |
| AB |
| EG |
| BH |
| 5 |
| 8 |
∴EG=
| 5 |
| 8 |
∴EF=EG+GF=
| 5 |
| 8 |
| 3 |
| 2 |
| 17 |
| 8 |
∵
| AB |
| a |
| DC |
| b |
∴
| BH |
| DC |
| AB |
| b |
| a |
∴
| EF |
| 17 |
| 8 |
| b |
| a |
故答案为：
| 17 |
| 8 |
| b |
| a |
点评：本题考查了平面向量，梯形，梯形的问题，难点在于作辅助线构造出平行四边形和三角形，本题关键在于作梯形腰的平行线并用BH表示出EF，平面向量的问题，熟记平行四边形法则和三角形法则是解题的关键．
练习册系列答案
课堂全解字词句段篇章系列答案
步步高口算题卡系列答案
相关题目
如图，BD、CE是△ABC的高，D、E为垂足，在BD上截取BF，使BF=AC，在CE的延长线取一点G，使CG=AB．试说明：①AF=AG；②AG⊥AF．某同学生日聚会，见面时每两个同学都互相握手了一次，共握手了36次，则参加此次聚会的人数是（ ）
| A、10人 | B、9人 | C、8人 | D、7人 |