题目内容
若四个互不相等的正实数a,b,c,d满足(a2012-c2012)(a2012-d2012)=2012,(b2012-c2012)(b2012-d2012)=2012,则(ab)2012-(cd)2012的值为
- A.-2012
- B.-2011
- C.2012
- D.2011
A
分析:根据题意可将a2012与b2012看做方程(x-c2012)(x-d2012)=2012的两个解,把所求的式子被减数利用积的乘方逆运算变形后换为x1x2,把方程整理后,利用根与系数的关系表示出x1x2,代入整理后的式子中,即可求出所求式子的值.
解答:设a2012与b2012看做方程(x-c2012)(x-d2012)=2012的两个解,
方程整理得:x2-(c2012+d2012)x+(cd)2012-2012=0,
则(ab)2012-(cd)2012=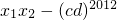 ,
,
又x1x2=(cd)2012-2012,
则(ab)2012-(cd)2012=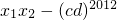 =(cd)2012-2012-(cd)2012=-2012.
=(cd)2012-2012-(cd)2012=-2012.
故选A.
点评:此题考查了根与系数的关系的运用,利用了方程的思想,其中当一元二次方程ax2+bx+c=0(a≠0)有解,即b2-4ac≥0时,设方程的两个根分别为x1,x2,则有x1+x2=- ,x1x2=
,x1x2= .
.
分析:根据题意可将a2012与b2012看做方程(x-c2012)(x-d2012)=2012的两个解,把所求的式子被减数利用积的乘方逆运算变形后换为x1x2,把方程整理后,利用根与系数的关系表示出x1x2,代入整理后的式子中,即可求出所求式子的值.
解答:设a2012与b2012看做方程(x-c2012)(x-d2012)=2012的两个解,
方程整理得:x2-(c2012+d2012)x+(cd)2012-2012=0,
则(ab)2012-(cd)2012=
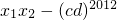 ,
,又x1x2=(cd)2012-2012,
则(ab)2012-(cd)2012=
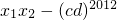 =(cd)2012-2012-(cd)2012=-2012.
=(cd)2012-2012-(cd)2012=-2012.故选A.
点评:此题考查了根与系数的关系的运用,利用了方程的思想,其中当一元二次方程ax2+bx+c=0(a≠0)有解,即b2-4ac≥0时,设方程的两个根分别为x1,x2,则有x1+x2=-
 ,x1x2=
,x1x2= .
. 
练习册系列答案
 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目