Question

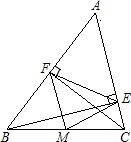
如图，BE、CF分别是△ABC的高，M为BC中点，BC=10，EF=5

2

，求△EFM的面积．

Answer 1

过M作MD⊥EF于D，
∵BE、CF分别是△ABC的高，
∴∠BFC=∠BEC=90°，
∵M为BC的中点，BC=10，
∴ME=MF=5，
∵EF=5

2

，
∴DE=DF=

5 2

2

，
在△MDE中由勾股定理得：MD=

52-( 5 2 2 )2

=

5 2

2

，
∴△EFM的面积是

1

2

EF•DM=

1

2

×5

2

×

5 2

2

=

25

2

．
答：△EFM的面积是

25

2

．