题目内容
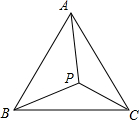
证明题：如图所示，在△ABC中，AB=AC，∠APB≠∠APC，求证：PB≠PC．
证明：假设PB≠PC不成立，则PB=PC，∠PBC=∠PCB；
又∵AB=AC，
∴∠ABC=∠ACB；
∴∠ABP=∠ACP；
∴△ABP≌△ACP，
∴∠APB=∠APC；
与∠APB≠∠APC相矛盾．因而PB=PC不成立，则PB≠PC．
分析：运用反证法进行求解：
（1）假设结论PB≠PC不成立，PB=PC成立．
（2）从假设出发推出与已知相矛盾．
（3）得到假设不成立，则结论成立．
点评：解此题关键要懂得反证法的意义及步骤．
又∵AB=AC，
∴∠ABC=∠ACB；
∴∠ABP=∠ACP；
∴△ABP≌△ACP，
∴∠APB=∠APC；
与∠APB≠∠APC相矛盾．因而PB=PC不成立，则PB≠PC．
分析：运用反证法进行求解：
（1）假设结论PB≠PC不成立，PB=PC成立．
（2）从假设出发推出与已知相矛盾．
（3）得到假设不成立，则结论成立．
点评：解此题关键要懂得反证法的意义及步骤．
练习册系列答案
相关题目
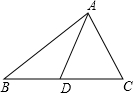（1）如图所示，在△ABC中，AD是BC边上的中线，且AD=
7、证明题：如图所示，在△ABC中，AB=AC，∠APB≠∠APC，求证：PB≠PC．
25、友情提示：本题有A、B两题，请你任选一题作答，A题满分9分，B题满分12分．若两题都做，只能按A题评分．
