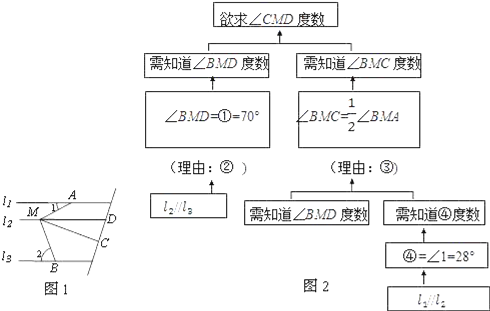
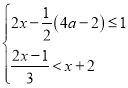��Ŀ����
����Ŀ����ͼ����ABC���Ϊ1����һ�β������ֱ��ӳ�AB��BC��CA����A1��B1��C1��ʹA1B��AB��B1C��BC��C1A��CA��˳������A1��B1��C1���õ���A1B1C1���ڶ��β������ֱ��ӳ�A1B1��B1C1��C1A1����A2��B2��C2��ʹA2B1��A1B1��B2C1��B1C1��C2A1��C1A1��˳������A2��B2��C2���õ���A2B2C2�������˹��ɣ�Ҫʹ�õ��������ε��������2019�����پ������������β�����
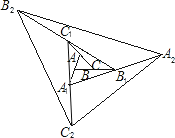
A.4B.5C.6D.7
���𰸡�A
��������
�ȸ�����֪���������![]() ����
����![]() ��������ٸ����������εı�����ϵ��⼴�ɣ�
��������ٸ����������εı�����ϵ��⼴�ɣ�
�⣺![]() ���
���![]() �����
�����![]() ����Ϊ
����Ϊ![]() ���������Ϊ
���������Ϊ![]() ��
��
![]() ���Ϊ1��
���Ϊ1��
![]() ��
��
ͬ���ɵã�![]() ��
��![]() ��
��
![]() ��
��
ͬ����֤��![]() �����
�����![]() ��
��![]() �����
�����![]() ��
��
�����β���������Ϊ![]() ��
��
���Ĵβ���������Ϊ![]() ��
��
�ʰ��˹��ɣ�Ҫʹ�õ��������ε��������2019�����پ���4�β�����
��ѡ��![]() ��
��

��ϰ��ϵ�д�
�����Ŀ