题目内容
【题目】如图,在直角坐标系中,⊙A的圆心A的坐标为(﹣1,0),半径为1,点P为直线y=﹣ ![]() x+3上的动点,过点P作⊙A的切线,切点为Q,则切线长PQ的最小值是 .
x+3上的动点,过点P作⊙A的切线,切点为Q,则切线长PQ的最小值是 . 
【答案】2 ![]()
【解析】解: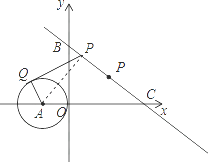
如图,作AP⊥直线y=﹣ ![]() x+3,垂足为P,作⊙A的切线PQ,切点为Q,此时切线长PQ最小∵A的坐标为(﹣1,0),
x+3,垂足为P,作⊙A的切线PQ,切点为Q,此时切线长PQ最小∵A的坐标为(﹣1,0),
设直线与x轴,y轴分别交于B,C,
∴B(0,3),C(4,0),
∴OB=3,AC=5,
∴BC= ![]() =5,
=5,
∴AC=BC,
在△APC与△BOC中, 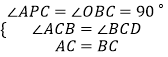 ,
,
∴△APC≌△OBC,
∴AP=OB=3,
∴PQ= ![]() =2
=2 ![]() .
.
过点A作AP⊥直线y=﹣ ![]() x+3,垂足为P,作⊙A的切线PQ,切点为Q,此时切线长PQ最小。用角角边可证△APC≌△OBC,根据全等三角形的性质可得AP=OB,在直角三角形APQ中用勾股定理可求PQ的长。
x+3,垂足为P,作⊙A的切线PQ,切点为Q,此时切线长PQ最小。用角角边可证△APC≌△OBC,根据全等三角形的性质可得AP=OB,在直角三角形APQ中用勾股定理可求PQ的长。

练习册系列答案
相关题目
【题目】![]() 朗读者
朗读者![]() 自开播以来,以其厚重的文化底蕴和感人的人文情怀,感动了数以亿计的观众,岳池县某中学开展“朗读”比赛活动,九年级
自开播以来,以其厚重的文化底蕴和感人的人文情怀,感动了数以亿计的观众,岳池县某中学开展“朗读”比赛活动,九年级![]() 、
、![]() 班根据初赛成绩,各选出5名选手参加复赛,两个班各选出的5名选手的复赛成绩
班根据初赛成绩,各选出5名选手参加复赛,两个班各选出的5名选手的复赛成绩![]() 满分为100分
满分为100分![]() 如图所示.
如图所示.
平均数 | 中位数 | 众数 | |
九 | 85 | 85 | |
九 | 80 |
![]() 根据图示填写表格;
根据图示填写表格;
![]() 结合两班复赛成绩的平均数和中位数,分析哪个班级的复赛成绩较好;
结合两班复赛成绩的平均数和中位数,分析哪个班级的复赛成绩较好;
![]() 如果规定成绩较稳定班级胜出,你认为哪个班级能胜出?说明理由.
如果规定成绩较稳定班级胜出,你认为哪个班级能胜出?说明理由.