题目内容
【题目】如图，点O是直线AB上一点，∠AOC=40°，OD平分∠AOC，∠COE=70°．
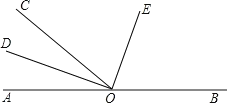
（1）请你说明DO⊥OE；
（2）OE平分∠BOC吗？为什么？
【答案】（1）证明见解析（2）证明见解析
【解析】
试题（1）根据角平分线的定义求得∠COD=20°，再根据垂线的定义证明；
（2）求得∠BOC的度数，根据角平分线的定义即可求得OE平分∠BOC．
试题解析：（1）∵OD平分∠AOC，
∴∠DOC=
∠AOC=20．
∵∠COE=70°，
∴∠DOE=90°，
∴DO⊥OE．
（2）OE平分∠BOC．
理由：∵∠AOC+∠COE+∠BOE=180°，
又∵∠AOC=40°，∠COE=70°，
∴∠BOE=70°，
∴∠BOE=∠COE，
∴OE平分∠BOC．
练习册系列答案
相关题目
