Question

如图，直角梯形ABCD中，AB∥CD，∠A=90°，AB=6，AD=4，DC=3，动点P从点A出发，沿A→D→C→B方向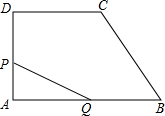移动，动点Q从点A出发，在AB边上移动．设点P移动的路程为x，点Q移动的路程为y，线段PQ平分梯形ABCD的周长．
（1）求y与x的函数关系式，并求出x，y的取值范围；
（2）当PQ∥AC时，求x，y的值；
（3）当P不在BC边上时，线段PQ能否平分梯形ABCD的面积？若能，求出此时x的值；若不能，说明理由．

Answer 1

分析：（1）过C作CE⊥AB于E，由勾股定理求得BC的值，进而得到梯形的周长为18，由题意知，y=-x+9，由于点Q只在AB上，于是能确定出x的取值范围；
（2）∵PQ∥AC，∴△BPQ∽△BCA，有

BP

BC

=

BQ

BA

，得6x-5y=42，与y=-x+9组成方程组求解即可；
（3）通过讨论点P的位置，建立关于x，y的方程组求得x的值．

解答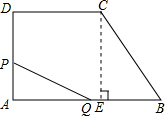：解：（1）过C作CE⊥AB于E，则CD=AE=3，CE=4，可得BC=5，
所以梯形ABCD的周长为6+3+4+5=18，
PQ平分ABCD的周长，所以x+y=9，
因为0≤y≤6，所以3≤x≤9，
所求关系式为：y=-x+9，3≤x≤9；

（2）依题意，P只能在BC边上，7≤x≤9．
PB=12-x，BQ=6-y，
因为PQ∥AC，所以△BPQ∽△BCA，所以

BP

BC

=

BQ

BA

，得：

12-x

5

=

6-y

6

，即6x-5y=42，
解方程组

x+y=9 6x-5y=42

得x=

87

11

，y=

12

11

；

（3）梯形ABCD的面积为18，
当P不在BC边上，则3≤x≤7，
（a）当3≤x＜4时，P在AD边上，S_△APQ=

1

2

xy，
如果线段PQ能平分梯形ABCD的面积，则有

1

2

xy=9，
可得：

x+y=9 xy=18

，解得

x=3 y=6

，

x=6 y=3

（舍去），
（b）当4≤x≤7时，点P在DC边上，此时S_ADPQ=

1

2

×4（x-4+y），
如果线段PQ能平分梯形ABCD的面积，则有

1

2

×4（x-4+y）=9，
可得

x+y=9 2x+2y=17

此方程组无解．
所以当x=3时，线段PQ能平分梯形ABCD的面积．

点评：本题利用了梯形的性质，相似三角形的判定和性质，三角形的面积公式，建立方程和方程组求解，注意要针对不同情况讨论，本题还利用数形结合的思想．