题目内容
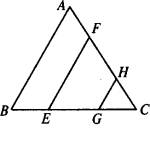
如图，在□ABCD中，点E、F在对角线AC上，且AE=CF．请你以F为一个端点，和图中已标明字母的某一点连成一条新线段，猜想并证明它和图中已有的某一条线段相等(只需证明一组线段相等即可)．(1)连结________．
(2)猜想：________=________．
(3)证明：
答案：
解析：
提示：
解析：
| 解法一：(1)BF
(2)BF DE
(3)证明：连结DB、DF，设DB、AC交于点O， ∵四边形ABCD是平行四边形，∴AO=OC，DO=OB． ∵AE=FC，∴AO-AE=OC-FC．∴EO=FO． ∴四边形EBFD为平行四边形．∴BF=DE． 解法二：(1)DF (2)DF BE (3)证明略 说明：(1)本例解法一中又可通过△BCF≌△DAE等证明BF=DE． (2)本例是结论猜想型的题目，此类题型是中考中常见题型．
|
提示：
| 导析：容易猜想连结BF，证明BF=DE．如图，可连结DF、DB，利用“对角线互相平分的四边形是平行四边形”判定四边形EBFD是平行四边形，从而证明猜想的结论．又可猜想连结DF，证明DF=BE，证明方法可同上面猜想结论的证明方法．
|
练习册系列答案
名校课堂系列答案
相关题目
，求DE的长。