Question

【题目】如图，在平面直角坐标系中，已知Rt△AOB的两条直角边OA、OB分别在y轴和x轴上，并且OA、OB的长分别是方程x2－7x＋12=0的两根（OA＜OB），动点P从点A开始在线段AO上以每秒1个单位长度的速度向点O运动；同时，动点Q从点B开始在线段BA上以每秒2个单位长度的速度向点A运动，设点P、Q运动的时间为t秒.

（1）求A、B两点的坐标.

（2）求当t为何值时，△APQ与△AOB相似?

Answer 1

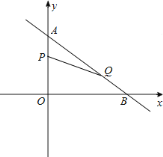
【答案】（1）A（0，3），B（4，0）；

（2）当t=或 t=时，△APQ与△AOB相似.

【解析】

（1）根据题意解方程即可得到A、B两点的坐标；

（2）根据题意在RT△AOB中，先求出AB，然后再把AP和AQ分别用t表示出来，根据相似三角形的性质求出t即可，应注意分两种情况讨论.

（1）解方程x2-7x+12=0，即（x-3）（x-4）=0,解得x1=3，x2=4，

∵OA＜OB，

∴OA=3，OB=4．

∴A（0，3），B（4，0）；

（2）在RT△AOB中，OA=3，OB=4，

∴AB=5，

∴AP=t，QB=2t，AQ=5-2t.

当△APQ∽△AOB时，

即 ，

解得t=；

当△APQ∽△ABO时，

即 ，

解得t=.

综上所述：当t=或 t=时，△APQ与△AOB相似.