题目内容

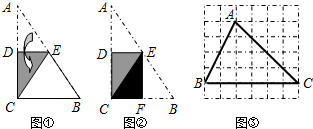
将一块直角三角形纸片ABC折叠，使点A与点C重合，展开后平铺在桌面上（如图所示）．若∠C=90°，BC=8cm，则折痕DE的长度是

cm．

分析：根据图形翻折变换的性质可知DE是AC的垂直平分线，由于∠C是直角，故∠AED=90°，进而可得出DE是△ABC的中位线，由中位线定理即可得出结论．

解答：解：∵点A与点C重合，
∴DE是AC的垂直平分线，
∵∠C是直角，
∴∠AED=90°，
∴DE是△ABC的中位线，
∴DE=

BC=

×8=4cm．
故答案为：4．

点评：本题考查的是翻折变换及三角形中位线定理，熟知图形翻折变换的性质是解答此题的关键．

练习册系列答案

励耘活页系列答案

将一块直角三角形纸片ABC折叠，使点A与点C重合，展开后平铺在桌面上（如

图所示）．若∠C＝90°，BC＝8cm，则折痕DE的长度是 cm．

将一块直角三角形纸片ABC折叠，使点A与点C重合，展开后平铺在桌面上（如

图所示）．若∠C＝90°，BC＝8cm，则折痕DE的长度是 cm．

在八年级探究“直角三角形斜边上的中线等于斜边的一半”这个结论时，我们是将一块直角三角形纸片按照图①方法折叠（点A与点C重合，DE为折痕）．再将图①中的△CBE沿对称轴EF折叠（如图②），通过折叠，可以发现CE=AE=BE= $数学公式$ AB．
（1）在上述的折叠过程中，我们还可以发现原三角形恰好折成两个重合的矩形，其中一个是内接矩形，另一个是拼合（指无缝无重叠）所成的矩形，我们称这样的两个矩形为“组合矩形”．你能将图③中的△ABC折叠成一个组合矩形吗？如果能折成，请在图③中画出折痕；
（2）有一些特殊的四边形，如菱形，通过折叠也能折成组合矩形（其中的内接矩形的四个顶点分别在原四边形的四条边上）．请你进一步探究，一个非特殊的四边形（指除平行四边形、梯形外的四边形）满足什么条件时，一定能折成组合矩形？
满足的条件是______．

试题分类