题目内容
嘉淇同学用配方法推导一元二次方程ax2+bx+c=0(a≠0)的求根公式时,对于b2﹣4ac>0的情况,她是这样做的:
由于a≠0,方程ax2++bx+c=0变形为:
x2+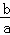 x=﹣
x=﹣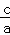 ,…第一步
,…第一步
x2+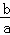 x+(
x+( )2=﹣
)2=﹣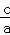 +(
+( )2,…第二步
)2,…第二步
(x+ )2=
)2=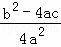 ,…第三步
,…第三步
x+ =
=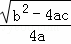 (b2﹣4ac>0),…第四步
(b2﹣4ac>0),…第四步
x= ,…第五步
,…第五步
嘉淇的解法从第 四 步开始出现错误;事实上,当b2﹣4ac>0时,方程ax2+bx+c=0(a≠O)的求根公式是 x=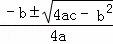 .
.
用配方法解方程:x2﹣2x﹣24=0.
解:在第四步中,开方应该是x+ =±
=± .所以求根公式为:x=
.所以求根公式为:x= .
.
故答案是:四;x= ;
;
用配方法解方程:x2﹣2x﹣24=0
解:移项,得
x2﹣2x=24,
配方,得
x2﹣2x+1=24+1,
即(x﹣1)2=25,
开方得x﹣1=±5,
∴x1=6,x2=﹣4.

练习册系列答案
相关题目
某种正方形合金板材的成本y(元)与它的面积成正比,设边长为x厘米.当x=3时,y=18,那么当成本为72元时,边长为( )
|
| A. | 6厘米 | B. | 12厘米 | C. | 24厘米 | D. | 36厘米 |
五名学生投篮球,规定每人投20次,统计他们每人投中的次数.得到五个数据.若这五个数据的中位数是6.唯一众数是7,则他们投中次数的总和可能是( )
|
| A. | 20 | B. | 28 | C. | 30 | D. | 31 |