题目内容
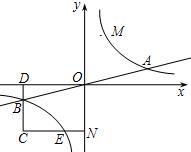 已知双曲线y=
已知双曲线y= 与直线y=
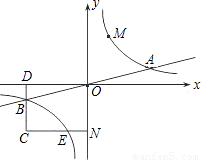
与直线y=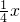 相交于A,B两点.第一象限上的点M(m,n)(在A点左侧)是双曲线y=
相交于A,B两点.第一象限上的点M(m,n)(在A点左侧)是双曲线y= 上的动点.过点B作BD∥y轴交x轴于点D.过N(0,-n)作NC∥x轴交双曲线y=
上的动点.过点B作BD∥y轴交x轴于点D.过N(0,-n)作NC∥x轴交双曲线y= 于点E,交BD于点C.若B是CD的中点,四边形OBCE的面积为4,则直线CM的解析式为________.
于点E,交BD于点C.若B是CD的中点,四边形OBCE的面积为4,则直线CM的解析式为________.
y=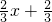
分析:根据一次函数和反比例函数的性质及点的坐标和解析式的关系解答.
解答:设B点坐标为(x1,- ),代入y=
),代入y= x得,-
x得,- =
= x1,x1=-2n;
x1,x1=-2n;
∴B点坐标为(-2n,- ).
).
因为BD∥y轴,所以C点坐标为(-2n,-n).
因为四边形ODCN的面积为2n•n=2n2,三角形ODB,三角形OEN的面积均为 ,四边形OBCE的面积为4.
,四边形OBCE的面积为4.
则有2n2-k=4---①;
又因为2n• =k,即n2=k---②
=k,即n2=k---②
②代入①得,4=2k-k,解得k=4;则解析式为y= ;
;
又因为n2=4,故n=2或n=-2.
M在第一象限,n>0;
将M(m,2)代入解析式y= ,得m=2.故M点坐标为(2,2);C(-4,-2);
,得m=2.故M点坐标为(2,2);C(-4,-2);
设直线CM解析式为y=kx+b,则 ,
,
解得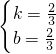
∴一次函数解析式为:y= x+
x+ .
.
点评:解答本题要明确两个关系:(1)双曲线中,xy=k;
(2)S△DBO= |k|.
|k|.
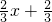
分析:根据一次函数和反比例函数的性质及点的坐标和解析式的关系解答.
解答:设B点坐标为(x1,-
 ),代入y=
),代入y= x得,-
x得,- =
= x1,x1=-2n;
x1,x1=-2n;∴B点坐标为(-2n,-
 ).
).因为BD∥y轴,所以C点坐标为(-2n,-n).
因为四边形ODCN的面积为2n•n=2n2,三角形ODB,三角形OEN的面积均为
 ,四边形OBCE的面积为4.
,四边形OBCE的面积为4.则有2n2-k=4---①;
又因为2n•
 =k,即n2=k---②
=k,即n2=k---②②代入①得,4=2k-k,解得k=4;则解析式为y=
 ;
;又因为n2=4,故n=2或n=-2.
M在第一象限,n>0;
将M(m,2)代入解析式y=
 ,得m=2.故M点坐标为(2,2);C(-4,-2);
,得m=2.故M点坐标为(2,2);C(-4,-2);设直线CM解析式为y=kx+b,则
 ,
,解得
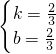
∴一次函数解析式为:y=
 x+
x+ .
.点评:解答本题要明确两个关系:(1)双曲线中,xy=k;
(2)S△DBO=
 |k|.
|k|. 
练习册系列答案
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案
相关题目
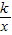 与直线y=
与直线y=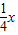 相交于A、B两点.第一象限上的点M(m,n)(在A点左侧)是双曲线y=
相交于A、B两点.第一象限上的点M(m,n)(在A点左侧)是双曲线y=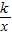 上的动点.过点B作BD∥y轴交x轴于点D.过N(0,-n)作NC∥x轴交双曲线y=
上的动点.过点B作BD∥y轴交x轴于点D.过N(0,-n)作NC∥x轴交双曲线y=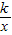 于点E,交BD于点C.
于点E,交BD于点C.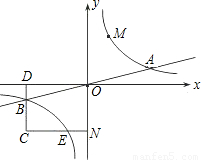
 与直线y=
与直线y= 相交于A,B两点.第一象限上的点M(m,n)(在A点左侧)是双曲线y=
相交于A,B两点.第一象限上的点M(m,n)(在A点左侧)是双曲线y=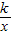 上的动点.过点B作BD∥y轴交x轴于点D.过N(0,-n)作NC∥x轴交双曲线y=
上的动点.过点B作BD∥y轴交x轴于点D.过N(0,-n)作NC∥x轴交双曲线y=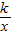 于点E,交BD于点C.若B是CD的中点,四边形OBCE的面积为4,则直线CM的解析式为 .
于点E,交BD于点C.若B是CD的中点,四边形OBCE的面积为4,则直线CM的解析式为 .
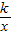 与直线y=
与直线y=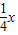 相交于A、B两点.第一象限上的点M(m,n)(在A点左侧)是双曲线y=
相交于A、B两点.第一象限上的点M(m,n)(在A点左侧)是双曲线y=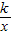 上的动点.过点B作BD∥y轴交x轴于点D.过N(0,-n)作NC∥x轴交双曲线y=
上的动点.过点B作BD∥y轴交x轴于点D.过N(0,-n)作NC∥x轴交双曲线y=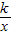 于点E,交BD于点C.
于点E,交BD于点C.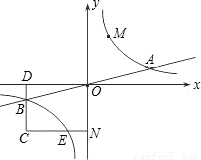
 与直线y=
与直线y=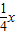 相交于A、B两点.第一象限上的点M(m,n)(在A点左侧)是双曲线y=
相交于A、B两点.第一象限上的点M(m,n)(在A点左侧)是双曲线y=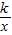 上的动点.过点B作BD∥y轴交x轴于点D.过N(0,-n)作NC∥x轴交双曲线y=
上的动点.过点B作BD∥y轴交x轴于点D.过N(0,-n)作NC∥x轴交双曲线y=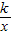 于点E,交BD于点C.
于点E,交BD于点C.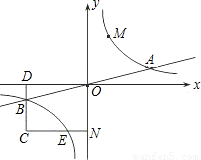
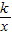 与直线y=
与直线y=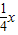 相交于A、B两点.第一象限上的点M(m,n)(在A点左侧)是双曲线y=
相交于A、B两点.第一象限上的点M(m,n)(在A点左侧)是双曲线y=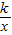 上的动点.过点B作BD∥y轴交x轴于点D.过N(0,-n)作NC∥x轴交双曲线y=
上的动点.过点B作BD∥y轴交x轴于点D.过N(0,-n)作NC∥x轴交双曲线y=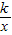 于点E,交BD于点C.
于点E,交BD于点C.