题目内容
在△ABC中，若AC=BC，∠ACB=90°，AB=10，则AC=________，AB边上的高CD=________．
5
5
分析：利用勾股定理求得AC的长度．然后根据面积法来求CD的长度．
解答：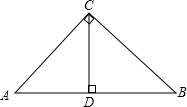
解：∵在△ABC中，若AC=BC，∠ACB=90°，AB=10，
∴AC2+BC2=AB2，即2AC2=100，
∴AC=5．
∵CD是AB边上的高线，
∴S△ABC=
AC•BC=AB•CD，
∴CD=
=
=5．
故答案是：5；5．
点评：本题考查了勾股定理．此题是等腰直角三角形，在求线段CD的长度时，也可以利用“直角三角形斜边上的中线等于斜边的一半”来求．
5分析：利用勾股定理求得AC的长度．然后根据面积法来求CD的长度．
解答：
解：∵在△ABC中，若AC=BC，∠ACB=90°，AB=10，∴AC2+BC2=AB2，即2AC2=100，
∴AC=5
．∵CD是AB边上的高线，
∴S△ABC=
AC•BC=AB•CD，∴CD=
==5．故答案是：5
；5．点评：本题考查了勾股定理．此题是等腰直角三角形，在求线段CD的长度时，也可以利用“直角三角形斜边上的中线等于斜边的一半”来求．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目