题目内容
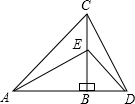如图，将两个一大、一小的等腰直角三角尺拼接 （A、B、D三点共线，AB=CB，EB=DB，∠ABC=∠EBD=90°），连接AE、CD，试确定AE与CD的位置与数量关系，并证明你的结论．分析：根据等腰直角三角形的性质得出△ABE≌△CBD即可得出AE与CD的位置与数量关系．
解答：
解：AE⊥CD，AE=CD，
理由：延长AE到CD上一点P，
∵在△ABE和△CBD中，
，
∴△ABE≌△CBD（SAS），
∴AE=DC，∠AEB=∠CDB，∠DCB=∠EAB，
∵∠EAB+∠AEB=90°，
∴∠AEB+∠DCB=90°，
∵∠AEB=∠CEP，
∴∠BCD+∠CEP=90°，
∴AE⊥CD．
解：AE⊥CD，AE=CD，理由：延长AE到CD上一点P，
∵在△ABE和△CBD中，
|
∴△ABE≌△CBD（SAS），
∴AE=DC，∠AEB=∠CDB，∠DCB=∠EAB，
∵∠EAB+∠AEB=90°，
∴∠AEB+∠DCB=90°，
∵∠AEB=∠CEP，
∴∠BCD+∠CEP=90°，
∴AE⊥CD．
点评：此题主要考查了等腰直角三角形的性质以及全等三角形的判定与性质，得出△ABE≌△CBD是解题关键．
练习册系列答案
小学课时特训系列答案
相关题目
针所指扇形上的数字之和为偶数，则甲胜；若数字之和为奇数，则乙胜．这个游戏对甲、乙两人公平吗？请说明理由．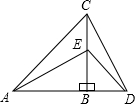
如图，将两个一大、一小的等腰直角三角尺拼接 （A、B、D三点共线，AB=CB，EB=DB，∠ABC=∠EBD=90°），连接AE、CD，试确定AE与CD的位置与数量关系，并证明你的结论．
