Question

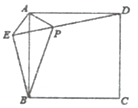
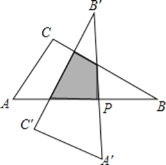
【题目】如图，在中，已知：，，，以斜边AB的中点P为旋转中心，把这个三角形按逆时针方向旋转得到，则旋转前后两个直角三角形重叠部分的面积为______．

Answer 1

【答案】

【解析】

根据已知及勾股定理求得DP的长，再根据全等三角形的判定得到△B′PH≌△BPD，从而根据直角三角形的性质求得GH，BG的长，从而不难求得旋转前后两个直角三角形重叠部分的面积．

解：如图，

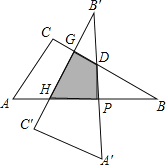
在直角△DPB中，BP=AP=AC=3，

∵∠A=60°，

∴DP2+BP2=BD2，

∴x2+32=（2x）2，

∴DP=x=，

∵在△B′PH和△BPD中， ，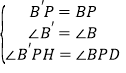

∴△B′PH≌△BPD，

∴PH=PD=，

∵在直角△BGH中，BH=3+，

∴GH=，BG=（3+），

∴S△BGH=××（3+）=，S△BDP=×3×=，

∴SDGHP=-，

=cm2．

故答案是：．