题目内容
 如图,
如图, |
| BC |
 |
| BC |
A、
| ||||||||
B、
| ||||||||
C、
| ||||||||
D、
|
分析:根据题意,得四边形AODC的最小面积即是三角形AOC的面积,最大面积即是当OD⊥OC时四边形的面积.
要求三角形AOC的面积,作CD⊥AO于D.根据等边三角形的性质以及直角三角形的性质,求得CD=
,得其面积是
;要求最大面积,只需再进一步求得三角形DOC的面积,即是
,则最大面积是
.
要求三角形AOC的面积,作CD⊥AO于D.根据等边三角形的性质以及直角三角形的性质,求得CD=
| ||
| 2 |
| ||
| 4 |
| 1 |
| 2 |
2+
| ||
| 4 |
解答: 解:根据题意,得四边形AODC的面积最小即是三角形AOC的面积,最大面积即是当OD⊥OC时四边形的面积.
解:根据题意,得四边形AODC的面积最小即是三角形AOC的面积,最大面积即是当OD⊥OC时四边形的面积.
作CH⊥AO于H,
∵△AOC为等边三角形
∴CH=
∴S△AOC=
;
当OD⊥OC时面积最大,
∴S△OCD=
,则最大面积是
+
=
∴四边形AODC的面积s的取值范围是
<s≤
.
故选B.
 解:根据题意,得四边形AODC的面积最小即是三角形AOC的面积,最大面积即是当OD⊥OC时四边形的面积.
解:根据题意,得四边形AODC的面积最小即是三角形AOC的面积,最大面积即是当OD⊥OC时四边形的面积.作CH⊥AO于H,
∵△AOC为等边三角形
∴CH=
| ||
| 2 |
∴S△AOC=
| ||
| 4 |
当OD⊥OC时面积最大,
∴S△OCD=
| 1 |
| 2 |
| ||
| 4 |
| 1 |
| 2 |
2+
| ||
| 4 |
∴四边形AODC的面积s的取值范围是
| ||
| 4 |
2+
| ||
| 4 |
故选B.
点评:此题首先要能够正确分析出要求的四边形的最小面积和最大面积,然后根据等边三角形的性质以及三角形的面积公式进行计算.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
如图,BC是半径为1的⊙O的弦,A为弧BC上一点,M、N分别为BD、AD的中点,则sin∠C的值等于( )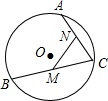

| A、AD | B、BC | C、MN | D、AC |


